Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины

ТРЕУГОЛЬНИК.

Площадь треугольника.

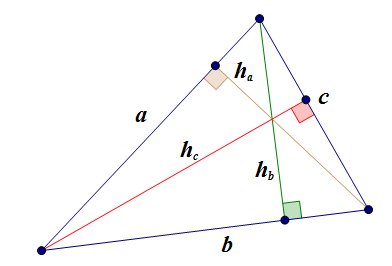
1. ,

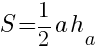здесь 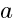- произвольная сторона треугольника, 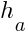- высота, опущенная на эту сторону.

2. ,

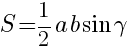здесь 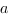и 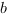- произвольные стороны треугольника, 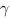- угол между этими сторонами:

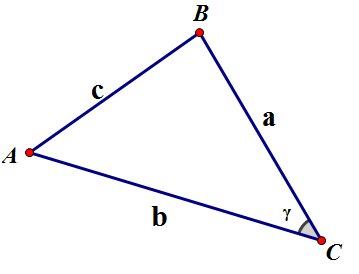
3. Формула Герона:

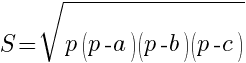
- здесь 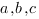- длины сторон треугольника, 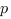- полупериметр треугольника,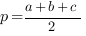

4. ,

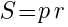здесь 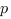- полупериметр треугольника, 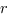- радиус вписанной окружности.

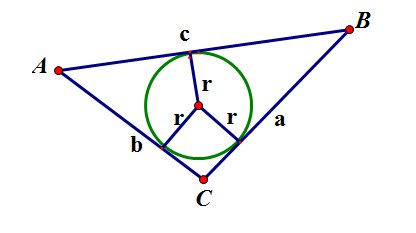
Пусть - длины отрезков касательных.

Тогда формулу Герона можно записать в таком виде:

5.

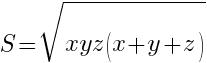
6. ,

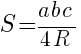здесь 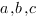- длины сторон треугольника, 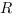- радиус описанной окружности.

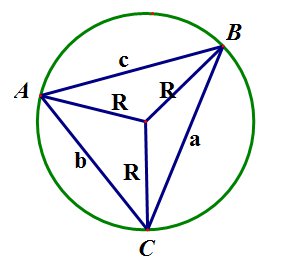
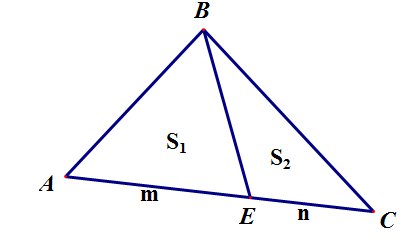
Если на стороне треугольника взята точка, которая делит эту сторону в отношении m:n, то отрезок, соединяющий эту точку с вершиной противолежащего угла делит треугольник на два треугольника, площади которых относятся как m:n:

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Медиана треугольника

- это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

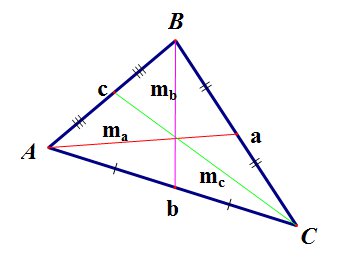
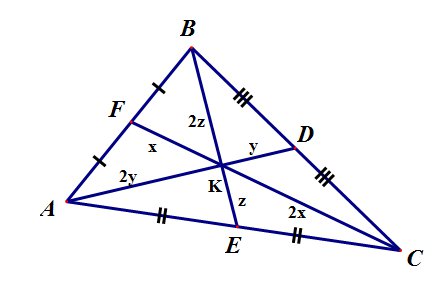
Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.

Точка пересечения медиан правильного треугольника делит медиану на два отрезка, меньший из которых равен радиусу вписанной окружности, а больший - радиусу описанной окружности.

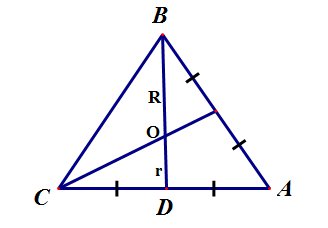Радиус описанной окружности в два раза больше радиуса вписанной окружности: R=2r

Длина медианы произвольного треугольника вычисляется по формуле:

,

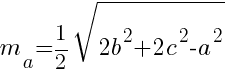здесь 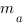- медиана, проведенная к стороне , 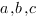- длины сторон треугольника.