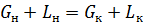2017-11-01
554
общий баланс
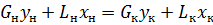баланс по распределяемому веществу
Возьмем произвольное сечение аппарата. Составим уравнение материального баланса нижней части аппарата:
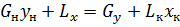
y- текущее значение, выразим
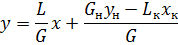
Полученное уравнение – уравнение рабочей линии.
В большинстве случаев считают, что количество фаз движущихся по аппарату практически постоянное (L=const; G=const)
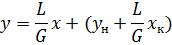
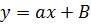- уравнение прямой линии.
Если мы принимаем допущение, что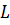 
и 
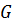постоянные, уравнение рабочей линии – прямая.
Если это допущение не принимаем (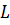 и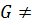 
const), уравнение рабочей линии - кривая.
Для всего аппарата в целом рабочие концентрации будут изменяться от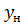 
до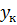 
в газовой фазе и то 
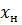до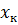 
в жидкой.
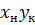- верх аппарата (координаты начала рабочей линии)
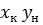- низ аппарата, крайние точки рабочей линии.
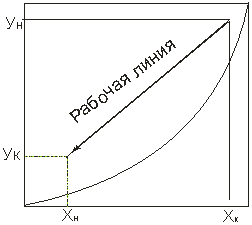
Объединим на одном графике рабочую и равновесную концентрации.
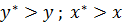
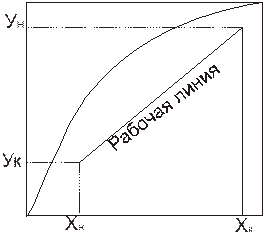Возьмем любую точку на аппарате с координатами х и у. Рабочая и равновесная линии никогда не пересекаются.Если рабочая линия выше равновесной – идет передача вещества из газовой в жидкую фазу.
Из жидкой в паровую фазу. Процесс перегонки.
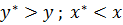
На графике можно определить движущую силу процесса:
1. Когда линия равновесия прямая или приближается к прямой.
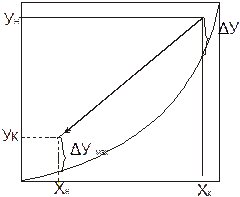
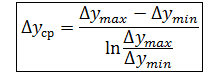
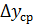- средняя движущая сила процесса по газовой фазе для всего аппарата.
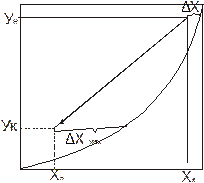
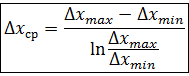
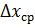- средняя движущая сила процесса по жидкой фазе.
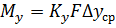
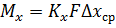
2. Если линия равновесия – кривая (на примере противоточного аппарата)
Рассмотрим процесс массопередачи протекающий в противоточном колонном аппарате при следующих условиях:
1) Зависимость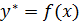 
- кривая.
2) L=const; G=const – расходы фаз по высоте аппарата постоянны – рабочая линия прямая.
3) 
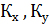по обеим фазам постоянны.
4) Рассмотрим процесс передачи вещества из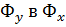 
(абсорбция).
5) При выводе будем выражать концентрации по фазе у (по газовой).
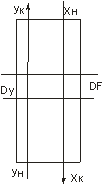
Выделим в аппарате элемент поверхности контакта dF.
В результате контакта на поверхности dF произойдет изменение концентрации dy в сторону уменьшения.
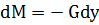
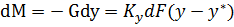
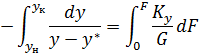
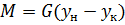
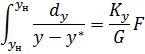
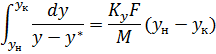
Сравним это выражение с основным уравнением массопередачи.
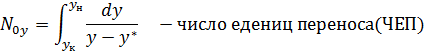
Выразим из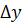 
ЧЕП:
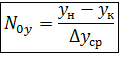
ЧЕП характеризует изменение рабочей концентрации фазы приходящейся на единицу движущей силы, т.е. 1 ед переноса можно рассмотреть как участок аппарата, для которого измененение концентрации одной из фаз равна средней движущей силе на этом участке ЧЕП может быть расписано по любой из фаз.
По фазе х:
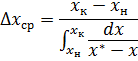
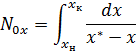
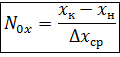
Определение ЧЕП.
1. Метод графического интегрирования:
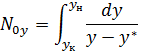
Последовательность определения ЧЕП методом графического интегрирования.
1) По справочным данным строим равновесную кривую
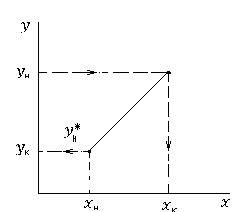
2) По данным материального баланса строим рабочую линию процесса.
3) Разбив интервал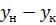 
на равные отрезки по графику заполняем таблицу:
| 
| 
| 
|
|
|
|
|
|
| |||
|
|
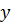
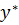
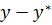
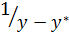
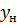
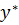
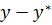
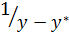
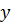
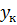
4) Определяем площадь кривой и с учетом масштабирования определяем ЧЕП.
2. Графический метод Бейкера.
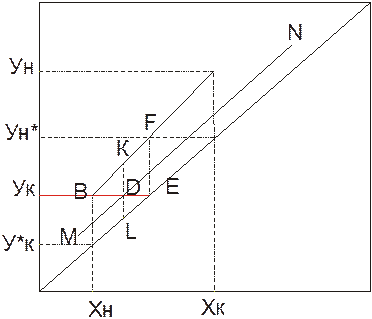
Используется если линия равновесия на участке соответветствующей одной единице переноса является прямой или имеет малую кривизну.
ЧЕП может быть записано как: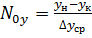 
1) Делим отрезк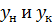и 
и 
пополам и через две точки проводим прямую.
Отрезок MN делит соответствующий аппарат пополам.
На продолжении отрезка BD откладываем отрезок равный BD(BD=DE). Из точки E проводим вертикальную линию за пересечение с рабочей линией процесса(EF) DL
Через точку D проводим вертикальную линию (DL,DK)
Докажем что EF=KL
Рассмотрим два треугольника: BEF и BDK – они подобны.
Т.к. BE=2BD; KD =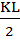 
. Отсюда следует что EF=KL.
Ступенька BEF соответствует участку аппарата, на котором изменение рабочих концентраций в фазе у равна средней движущей силе не этом участке. Т.е. этот треугольник является единицей переноса.
Аналогично, вписывая таким образом треугольники, находим число единиц переноса по всей длине аппарата.
