F1(x, y1, …., yn, y1’, …, yn’) = 0,
…………………………………
Fn(x, y1, …., yn, y1’, …, yn’) = 0,
- совокупность n функций y1(х), y2(х), …,yn (х), имеющих непрерывные производные и обращающих все уравнения этой системы в тождества.
Система обыкновенных дифференциальных уравнений -совокупность уравнений
F1(x, y1, …., yn, y1’, …, yn’) = 0,
…………………………………
Fn(x, y1, …., yn, y1’, …, yn’) = 0,
где y1(х), y2(х), …,yn (х) - искомые функции от x.
Система линейных обыкновенных дифференциальных уравнений - система обыкновенных дифференциальныхуравнений вида
 .
.
Теорема Пеано – см. Теорема существования решения задачи Коши.
Теорема существования решения задачи Коши (Теорема Пеано): Если правая часть дифференциального уравнения  определена и непрерывна по совокупности переменных в некоторой окрестности точки
определена и непрерывна по совокупности переменных в некоторой окрестности точки 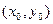 , то уравнение имеет хотя бы одно решение y = y(x), удовлетворяющее начальному условию y(x0) = x0.
, то уравнение имеет хотя бы одно решение y = y(x), удовлетворяющее начальному условию y(x0) = x0.
Теорема Пикара – см. Теорема существования и единственности решения задачи Коши.
Теорема существования и единственности решения задачи Коши (теорема Пикара): Если правая часть уравнения  определена в некоторой окрестности точки
определена в некоторой окрестности точки 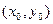 и удовлетворяет в ней двум условиям:
и удовлетворяет в ней двум условиям:
1) непрерывна по совокупности переменных;
2) имеет непрерывную частную производную по переменной у  ,
,
то уравнение имеет единственное решение y = y(x), удовлетворяющее начальномуусловию y(x0) = x0.
Уравнение Бернулли - уравнение вида
y’+ p(x)y = g(x)у(n),
где n – любое вещественное число, отличное от нуля и единицы.
Уравнение в полных дифференциалах - см .дифференциальное уравнение в полных дифференциалах.
Уравнение с частными производными - дифференциальное уравнение, в котором искомая неизвестная функция зависит от нескольких независимых переменных.
Формула Остроградского - Лиувилля - формула 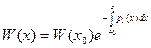 для определителя Вронского, составленного из n частных решений однородного линейного уравнения n-го порядка
для определителя Вронского, составленного из n частных решений однородного линейного уравнения n-го порядка 
его коэффициенты при производной порядка (n-1).
Фундаментальная система решений - система линейно независимых решений линейного дифференциального уравнения. Число линейно независимых решений в фундаментальной системе соответствует порядку уравнения.
Характеристическое уравнение для линейного дифференциального уравнения второго порядка с постоянными коэффициентами
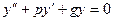 , (1)
, (1)
получается при замене  и имеет вид
и имеет вид
 .
.
Частное решение - решение, в каждой точке которого сохраняется единственность решения задачи Коши. Частное решение содержится в общем решении при определенных значениях С, включая С = ± ∞.
 2017-11-01
2017-11-01 534
534







