2017-11-01
314
«Определение областей устойчивости системы автоматического управления»
Цель работы:
1.1 Определение областей устойчивости систем автоматического управления методом Д-разбиения.
Содержания задания на контрольную работу:
1.1 Определить границы апериодической устойчивости и колебательной, если передаточная функция системы в разомкнутом состоянии в плоскости параметров 
и 
Коэффициенты передаточной функции определяются по табл. 16 и двум последним цифрам студенческого билета (зачетной книжки): 
- предпоследняя цифра (учитывается только четность или нечетность ); 
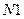-последняя цифра.
Таблица 16.
| ||||||||||
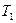
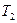
| 0,1 | 0,8 | 0,7 | 0,5 | 0,6 | 0,7 | 0,3 | 0,1 | 0,5 | 0,2 |
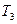
| 0,04 | 0,7 | 0,2 | 0,5 | 0,04 | 0,4 | 0,7 | 0,3 | 0,02 | 0,8 |
| N1 | ||||||||||
| N2 | Четная | |||||||||
|
| ||||||||||
|
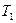
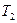
| 0,3 | 0,4 | 0,03 | 0,7 | 0,6 | 0,7 | 0,2 | 0,2 | 0,06 | 0,03 |
|
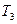
| 0,1 | 0,7 | 0,6 | 0,5 | 0,5 | 0,1 | 0,8 | 0,1 | 0,7 | 0,1 |
| N1 | ||||||||||
| N2 | Нечетная |
1.2 Используя Д-разбиение определить границу колебательной устойчивости при изменении параметров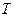 
и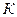 
, если передаточная функция разомкнутой системы равна:
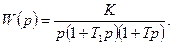
Коэффициенты передаточной функции определяются по табл. 17 и двум последним цифрам студенческого билета (зачетной книжки): - предпоследняя цифра (учитывается только четность или нечетность ); 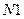- последняя цифра.
Таблица 17.
|
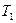
| 0,31 | 0,8 | 0,57 | 0,5 | 0,76 | 0,7 | 0,3 | 0,1 | 0,85 | 0,22 |
| N1 | ||||||||||
| N2 | Четная | |||||||||
|
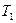
| 0,33 | 0,4 | 0,13 | 0,7 | 0,6 | 0,7 | 0,2 | 0,2 | 0,36 | 0,73 |
| N1 | ||||||||||
| N2 | Нечетная |
1.3 Используя критерий Гурвица, построить область устойчивости в плоскости координат 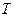и .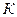
Рис. 4.
Параметры схемы определяются по табл. 18 и двум последним цифрам студенческого билета (зачетной книжки): - предпоследняя цифра (учитывается только четность или нечетность ); 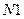- последняя цифра (она же является номером схемы на рис. 4).
Таблица 18.
| N2 | N1 | Передаточные функции | N2 | N1 | Передаточные функции | ||
| 
|
|
| ||||
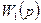
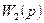
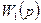
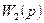
| Четная |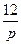 
| 
| Нечетная |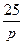 
| 
| ||
| 
| 
|
| ||||
|
| 
| 
|
| ||||
|
| 
|
|
| ||||
|
| 
| 
|
| ||||
|
|
|
| 
| ||||
|
| 
|
| ||||
|
|
| 
| ||||
|
|
|
| ||||
|
| 
| 
|
|
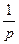
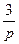
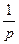
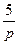
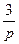
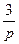
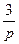
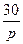
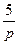
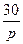
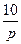
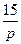
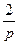
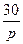
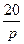
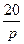
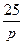
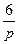
1.4 Используя критерий Михайлова, определить границу колебательной устойчивости при изменении параметров 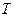и 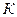, если передаточная функция разомкнутой системы равна:
Коэффициенты передаточной функции определяются по табл. 19 и двум последним цифрам студенческого билета (зачетной книжки): - предпоследняя цифра (учитывается только четность или нечетность ); 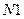- последняя цифра.
Таблица 19.
|
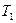
| 0,03 | 0,7 | 0,3 | 0,4 | 0,2 | 0,8 | 0,5 | 0,2 | 0,3 | 0,7 |
|
| 0,15 | 0,3 | 0,09 | 0,7 | 0,01 | 0,3 | 0,4 | 0,7 | 0,01 | 0,5 |
| N1 | ||||||||||
| N2 | Четная | |||||||||
|
| 0,2 | 0,7 | 0,05 | 0,1 | 0,05 | 0,8 | 0,7 | 0,1 | 0,08 | 0,03 |
|
| 0,4 | 0,7 | 0,75 | 0,5 | 0,75 | 0,1 | 0,8 | 0,3 | 0,45 | 0,5 |
| N1 | ||||||||||
| N2 | Нечетная |
1.5 Используя Д-разбиение определить колебательную границу устойчивости при изменении параметров 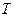и 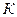, если передаточная функция разомкнутой системы равна:
Коэффициенты передаточной функции определяются по табл. 20 и двум последним цифрам студенческого билета (зачетной книжки): - предпоследняя цифра (учитывается только четность или нечетность ); 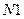- последняя цифра.
Таблица 20.
|
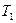
| 0,02 | 0,9 | 0,3 | 0,8 | 0,7 | 0,8 | 0,4 | 0,2 | 0,7 | 0,7 |
|
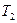
| 0,15 | 0,3 | 0,9 | 0,7 | 0,1 | 0,3 | 0,4 | 0,7 | 0,1 | 0,5 |
| N1 | ||||||||||
| N2 | Четная | |||||||||
|
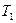
| 0,32 | 0,7 | 0,05 | 0,1 | 0,5 | 0,8 | 0,7 | 0,1 | 0,8 | 0,03 |
|
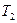
| 0,5 | 0,7 | 0,5 | 0,5 | 0,5 | 0,1 | 0,8 | 0,3 | 0,5 | 0,5 |
| N1 | ||||||||||
| N2 | Нечетная |
