«Исследование устойчивости систем автоматического управления»
Цель работы:
1.1 Закрепление знаний, полученных в процессе изучения основного лекционного курса, а также выполнение лабораторных работ, связанных с исследованием алгебраических и частотных критериев устойчивости САУ.
Содержания задания на контрольную работу:
1.1 Передаточная функция разомкнутой системы с запаздыванием имеет следующий вид:
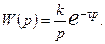
Используя критерии Найквиста оценить устойчивость САУ. Как повлияет на устойчивость уменьшение 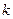 в 10 раз или увеличение
в 10 раз или увеличение 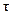 в 100 раз.
в 100 раз.
Коэффициенты передаточной функции определяются по табл. 7 и двум последним цифрам студенческого билета (зачетной книжки):  - предпоследняя цифра (учитывается только четность или нечетность
- предпоследняя цифра (учитывается только четность или нечетность  );
); 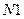 - последняя цифра.
- последняя цифра.
Таблица 7.
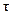
| 0,1 | 0,4 | 0,3 | 0,7 | 0,6 | 0,8 | 0,4 | 0,1 | 0,5 | 0,07 |
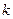
| 0,15 | 0,3 | 0,8 | 0,6 | 0,1 | 0,3 | 0,8 | 0,7 | 0,1 | 0,55 |
| N1 | ||||||||||
| N2 | Четная | |||||||||
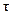
| 0,32 | 0,4 | 0,05 | 0,1 | 0,55 | 0,8 | 0,7 | 0,1 | 0,08 | 0,03 |
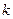
| 0,25 | 0,7 | 0,35 | 0,5 | 0,85 | 0,1 | 0,8 | 0,3 | 0,65 | 0,85 |
| N1 | ||||||||||
| N2 | Нечетная |
1.2 Передаточная функция в разомкнутом состоянии имеет вид:
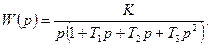
Определить устойчивость системы, используя критерий устойчивости Найквиста.
Коэффициенты передаточной функции определяются по табл. 8 и двум последним цифрам студенческого билета (зачетной книжки):  - предпоследняя цифра (учитывается только четность или нечетность
- предпоследняя цифра (учитывается только четность или нечетность  );
); 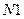 -последняя цифра.
-последняя цифра.
Таблица 8.
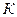
| ||||||||||
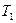
| 0,01 | 0,1 | 0,03 | 0,8 | 0,06 | 0,5 | 0,2 | 0,9 | 0,05 | 0,07 |
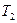
| 0,3 | 0,8 | 0,88 | 0,6 | 0,87 | 0,2 | 0,3 | 0,2 | 0,32 | 0,68 |
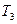
| 0,55 | 0,3 | 0,2 | 0,1 | 0,55 | 0,9 | 0,6 | 0,6 | 0,09 | 0,1 |
| N1 | ||||||||||
| N2 | Четная | |||||||||
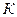
| ||||||||||
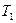
| 0,22 | 0,6 | 0,03 | 0,6 | 0,86 | 0,3 | 0,8 | 0,7 | 0,38 | 0,13 |
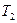
| 0,01 | 0,4 | 0,66 | 0,1 | 0,55 | 0,9 | 0,1 | 0,3 | 0,55 | 0,99 |
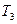
| 0,6 | 0,8 | 0,35 | 0,3 | 0,54 | 0,1 | 0,6 | 0,9 | 0,41 | 0,2 |
| N1 | ||||||||||
| N2 | Нечетная |
1.3 Используя критерий устойчивости Михайлова, определить устойчивость системы, передаточная функция которой в разомкнутом состоянии равна:

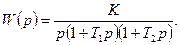
Коэффициенты передаточной функции определяются по табл. 9 и двум последним цифрам студенческого билета (зачетной книжки):  - предпоследняя цифра (учитывается только четность или нечетность
- предпоследняя цифра (учитывается только четность или нечетность  );
); 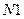 - последняя цифра.
- последняя цифра.
Таблица 9.
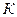
| ||||||||||
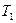
| 0,21 | 0,1 | 0,38 | 0,8 | 0,66 | 0,5 | 0,3 | 0,1 | 0,85 | 0,77 |
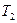
| 0,3 | 0,8 | 0,88 | 0,6 | 0,87 | 0,2 | 0,3 | 0,2 | 0,32 | 0,68 |
| N1 | ||||||||||
| N2 | Четная | |||||||||
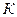
| ||||||||||
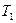
| 0,22 | 0,6 | 0,03 | 0,6 | 0,86 | 0,3 | 0,8 | 0,7 | 0,38 | 0,13 |
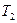
| 0,21 | 0,4 | 0,76 | 0,1 | 0,85 | 0,2 | 0,8 | 0,8 | 0,5 | 0,9 |
| N1 | ||||||||||
| N2 | Нечетная |
1.4 Использовать критерии Найквиста, исследовать устойчивость САУ:
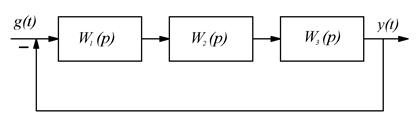
Рис. 3.
Параметры схемы определяются по табл. 10 и двум последним цифрам студенческого билета (зачетной книжки):  - предпоследняя цифра (учитывается только четность или нечетность
- предпоследняя цифра (учитывается только четность или нечетность  );
); 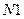 - последняя цифра (она же является номером схемы на рис. 3).
- последняя цифра (она же является номером схемы на рис. 3).
Таблица 10.
| N2 | N1 | Передаточные функции | N2 | N1 | Передаточные функции | ||||
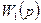
| 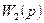
| 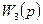
| 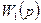
| 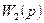
| 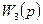
| ||||
| Четная | 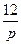
| 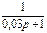
| 
| Нечетная | 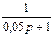
| 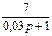
| 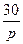
| ||
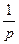
| 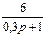
| 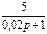
| 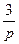
| 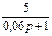
| 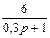
| ||||
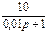
| 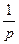
| 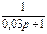
| 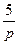
| 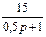
| 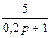
| ||||
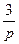
| 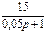
| 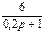
| 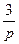
| 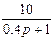
| 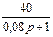
| ||||
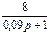
| 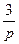
| 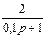
| 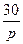
| 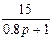
| 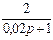
| ||||
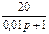
| 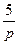
| 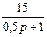
| 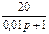
| 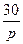
| 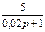
| ||||
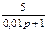
| 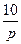
| 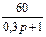
| 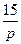
| 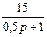
| 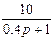
| ||||
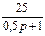
| 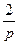
| 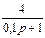
| 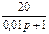
| 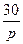
| 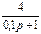
| ||||
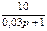
| 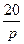
| 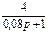
| 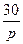
| 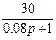
| 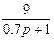
| ||||
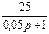
| 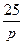
| 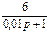
| 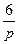
| 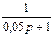
| 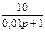
|
1.5 Используя критерий устойчивости по Гурвица, определить устойчивость замкнутой системы с отрицательной обратной связью, передаточная функция которой в разомкнутом состоянии равна:
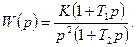
Коэффициенты передаточной функции определяются по табл. 11 и двум последним цифрам студенческого билета (зачетной книжки):  - предпоследняя цифра (учитывается только четность или нечетность
- предпоследняя цифра (учитывается только четность или нечетность  );
); 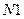 -последняя цифра.
-последняя цифра.
Таблица 11.
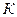
| ||||||||||
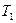
| 0,31 | 0,8 | 0,57 | 0,5 | 0,76 | 0,7 | 0,3 | 0,1 | 0,85 | 0,22 |
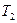
| 0,4 | 0,7 | 0,82 | 0,5 | 0,44 | 0,4 | 0,7 | 0,3 | 0,42 | 0,68 |
| N1 | ||||||||||
| N2 | Четная | |||||||||
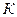
| ||||||||||
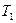
| 0,33 | 0,4 | 0,13 | 0,7 | 0,6 | 0,7 | 0,2 | 0,2 | 0,36 | 0,73 |
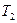
| 0,71 | 0,7 | 0,86 | 0,5 | 0,85 | 0,1 | 0,8 | 0,1 | 0,47 | 0,1 |
| N1 | ||||||||||
| N2 | Нечетная |
1.6 Используя критерий устойчивости Рауса, определить устойчивость системы, характеристическое уравнение системы имеет вид:
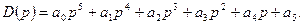
Коэффициенты характеристического уравнения определяются по табл. 12 и двум последним цифрам студенческого билета (зачетной книжки):  - предпоследняя цифра (учитывается только четность или нечетность
- предпоследняя цифра (учитывается только четность или нечетность  );
); 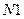 -последняя цифра.
-последняя цифра.
Таблица 12.
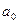
| ||||||||||
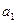
| ||||||||||
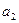
| ||||||||||
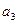
| ||||||||||
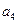
| ||||||||||
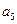
| ||||||||||
| N1 | ||||||||||
| N2 | Четная | |||||||||
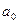
| ||||||||||
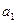
| ||||||||||
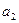
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| N1 | ||||||||||
| N2 | Нечетная |
 2017-11-01
2017-11-01 320
320








