Выполнение действий над комплексными числами
Цель занятия: формировать умение графического изображения комплексных чисел и выполнения арифметических операций с комплексными числами в алгебраической форме.
Указания к выполнению практической работы
| Пример. | Даны комплексные числа 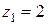 и и  .
а) Построить .
а) Построить  и и  в комплексной плоскости.
б) Найти в алгебраической форме в комплексной плоскости.
б) Найти в алгебраической форме  . .
|
Решение.
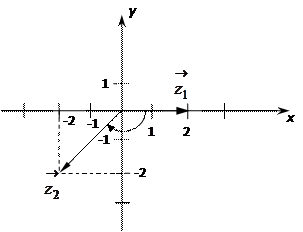 |
а) Изобразим комплексные числа на комплексной плоскости:
Число 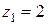 является чисто действительным числом (его мнимая часть равна нулю), оно изобразится вектором
является чисто действительным числом (его мнимая часть равна нулю), оно изобразится вектором  , лежащем на действительной оси (т.е. оси Ox).
, лежащем на действительной оси (т.е. оси Ox).
Число  изобразится вектором
изобразится вектором  , находящемся в III четверти.
, находящемся в III четверти.
б) Выполним действия в алгебраической форме записи:
1) 
2) 
3) 
4) 
Пример 2. Вычислить модуль и аргумент комплексные числа 
 |
Решение. 






|


Варианты практической работы
Даны комплексные числа  и
и  .
.
а) Построить  и
и  в комплексной плоскости.
в комплексной плоскости.
б) Найти в алгебраической форме  .
.
в) Вычислить модуль и аргумент комплексных чисел  и
и  .
.


Практическое занятие № 3
Нахождение математического ожидания.
Цель занятия: 1) знать формулы для вычисления математического ожидания:
2) уметь вычислять математическое ожидание случайной величины.
 2017-11-01
2017-11-01 326
326








