2017-11-01
395
Пример. Исследовать средствами дифференциального исчисления функцию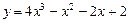 
и построить её график.
Решение. Проведём исследование заданной функции:
1)Найдём производную заданной функции 
.
2)Найдём интервалы возрастания и убывания функции, решив неравенства 
и 
соответственно.
, 
, 
при 
и 
, следовательно, при этих значениях x функция возрастает.
при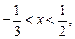 
следовательно, при этих значениях x функция убывает.
3) Найдём точки экстремумов функции: 
при 
и 
При переходе через точку знак 
меняется с «+» на «-», следовательно, точка является точкой максимума функции, причём
При переходе через точку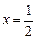 
знак меняется с «-» на «+», следовательно, точка 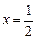является точкой минимума функции, причём 
.
4) Найдём 
и интервалы выпуклости и вогнутости графика функции, решив неравенства 
и 
соответственно.
; при 
, то есть при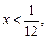 
следовательно, при 
график функции выпуклый; при 
, следовательно, при график функции вогнутый. Точка 
разделяет интервалы выпуклости и вогнутости графика функции, следовательно, является точкой перегиба графика функции, причём 
|
|
|
5) Так как функция определена при всех значениях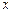 
, то её график не имеет точек разрыва и, следовательно, не имеет вертикальных асимптот.
Так как 
то наклонных асимптот график функции не имеет.
6) Строим график функции
Исследовать функцию 
и построить её график.
Решение. 1) Область определения 
.
2) Функция непрерывна во всей её области определения. Следовательно, нет ни точек разрыва, ни вертикальных асимптот.
3) Функция чётная, так как 
:
.
График функции симметричен относительно оси ординат.
4) Экстремумы и интервалы монотонности.
. Из уравнения 
получим три критические точки: 
. Исследуем характер критических точек. Для этого методом пробных точек определяем знак производной в каждом из интервалов: (- ∞; -1), (-1; 0), (0; 1), (1; + ∞).
На интервалах (-∞; -1) и (0; 1) функция убывает, на интервалах (-1; 0) и (1; +∞) – возрастает. При переходе через критические точки x1 = -1 и х3 = 1 производная меняет знак с минуса на плюс, следовательно, в этих точках функция имеет минимум. 
; 
.При переходе через критическую точку х = 0 производная меняет знак с плюса на минус. Следовательно, в этой точке функция имеет максимум уmax = ƒ(0)=5.
5) Интервалы выпуклости и точки перегиба.
. Из уравнения 
получим 
и 
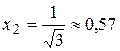. Определяем знак второй производной в каждом из интервалов:
, 
, 
.
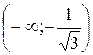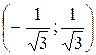Таким образом, кривая, вогнутая на интервалах 
и 
и выпуклая на интервале 
, а 
, 
– точки перегиба.
;
.
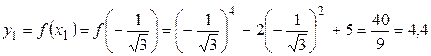6) Наклонная асимптота имеет вид у = kx + b, если существуют конечные пределы: 
, 
;
.
Таким образом, функция не имеет наклонных асимптот.
7) Дополнительные точки, уточняющие график:
|
|
|
; 
. Построим график функции:
Варианты практической работы
Исследовать функцию и построить график.
1. 
.
2. 
.
3. 
.
4. 
.
5. 
.
6. 
.
7. 
.
8. 
.
9. 
.
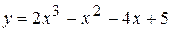10. 
.
Литература:
1. Пехлецкий И.Д. Математика: Учебник. - М.: Издательский центр "Академия", 2011. -304 с.- Серия: "Среднее профессиональное образование".
2. Богомолов Н.В. Практические занятия по математике. - М.: Наука, 1990.
3. Григорьев В. П. Элементы высшей математики. – М.: Издательский центр «Академия», 2004
4. Спирина М. С. Теория вероятностей и математическая статистика. – М.: Издательский центр «Академия», 2007
