Указания к выполнению практической работы

Пример. Найти математическое ожидание 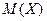, дисперсию и среднее квадратическое отклонение дискретной случайной величины 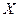, закон распределения которой задан в виде таблицы:

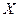
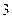
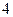
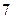
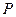
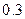
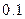
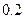
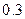
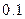
Решение. Математическое ожидание равно сумме произведений всех возможных значений 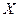на их вероятности: .

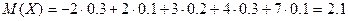Для вычисления дисперсии воспользуемся формулой: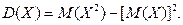

Составим закон распределения :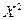

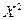
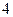
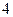
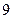
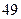
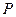
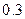
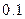
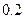
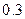
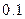
Найдем математическое ожидание : .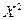

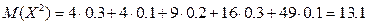Подставив в формулу для вычисления дисперси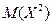и и 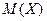найденное ранее, получим: .

Найдем искомое среднее квадратическое отклонение: .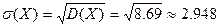

Варианты практической работы

Закон распределения дискретной случайной величины 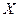задан в виде таблицы.

Найти: 1) математическое ожидание ;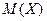

2) дисперсию ;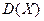

3) среднее квадратическое отклонение ;

4) начальные и центральные моменты первого, второго и третьего порядков.

Построить многоугольник распределения.

1.		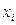						2.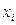
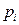
	0.2	0.3	0.2	0.1	0.2		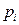	0.1	0.3	0.2	0.1	0.3
3.		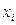						4.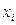
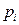
	0.2	0.3	0.1	0.2	0.2		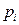	0.3	0.1	0.2	0.1	0.3
5.		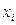						6.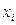
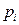
	0.1	0.4	0.1	0.3	0.1		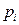	0.1	0.3	0.1	0.4	0.1
7.		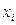						8.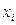
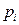
	0.2	0.3	0.1	0.3	0.1		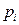	0.1	0.4	0.1	0.3	0.1
9.		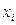						10.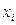
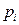
	0.1	0.2	0.1	0.5	0.1		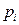	0.1	0.5	0.1	0.2	0.1

Практическое занятие № 4

Исследование функций с помощью производной

Цель занятия: 1) знать схему исследования функции;

2) уметь применять полученные сведения для построения графиков функций на основе предварительного исследования функции в соответствии со схемой.

Дидактическое оснащение практического занятия: методические рекомендации к выполнению работы