Указания к выполнению практической работы

Практическое занятие № 1

Вычисление определителей и выполнение действий над матрицами.

Нахождение матриц, обратных данным

Цель занятия: 1) знать правила вычисления определителей 2-го и 3-го порядка;

2) знать правила выполнения действий с матрицами;

3) знать алгоритм вычисления матрицы, обратной данной;

4) уметь вычислять определители 2-го и 3-го порядка;

5) уметь выполнять действия с матрицами;

6) уметь вычислять матрицу, обратной данной.

Указания к выполнению практической работы

Пример 1. Вычислить определитель .

Решение. Определитель второго порядка равен разности между произведениями элементов главной диагонали (a₁ и b₂) и побочной (b₁ и a₂), то есть

.

Поэтому .

Пример 2. Вычислить определитель .

Решение. Определитель третьего порядка можно вычислить по формуле

Получаем

.

Пример 3. Умножить матрицу на матрицу .

Решение. Известно, что матрицу A размера 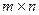(m − число строк, n − число столбцов) можно умножить на матрицу B размера , если n = p, причем в результате получится матрица размера . Элемент c_ij (расположен на пересечении i- й строки и j -го столбца) результирующей матрицы C вычисляется по формуле

,

то есть равен сумме произведений элементов строки i матрицы A на соответствующие элементы столбца j матрицы B.

В данной задаче матрицы A и B имеют размер и 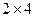соответственно, и, значит, перемножаемы (n=p= 2), а результирующая матрица C будет иметь размер .

Найдем c₁₁, для чего умножим поэлементно первую строку матрицы A на первый столбец матрицы B и результаты сложим:

.

Вычислим c₁₂, умножив первую строку матрицы A на второй столбец матрицы B и сложив результаты:

.

Аналогично, находим остальные элементы

,

,

,

.

Итак,

.

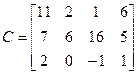Пример 4. Выполнить действия с матрицами: 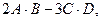где

Решение. Устанавливаем возможность выполнения указанных действий. Матрица А имеет порядок 3×5, матрица В - 5×2. Умножение возможно, поскольку число столбцов первой матрицы равно числу строк второй; в результате умножения получится матрица порядка 3×2. У второго произведения матрица С имеет порядок 3×4, матрица D - 4×2, умножение возможно, итоговая матрица будет иметь порядок 3×2. Сложение первого произведения со вторым также возможно, ибо оба произведения есть матрицы порядка 3×2.

Следовательно

где

Итак,

2) где

Итак,

Тогда,

Ответ:

Пример 5. Найти матрицу, обратную матрице .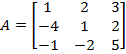

Решение. Найдем определитель матрицы А:

∆

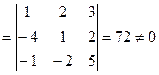
Следовательно, матрица А имеет обратную матрицу.

Обратная матрица определяется по формуле

= ,

где алгебраические дополнения элементов данной матрицы А.

Найдем алгебраические дополнения для элементов матрицы А:

Обратная матрица имеет вид

Необходимо сделать проверку

т.е.

Варианты практической работы

Задание №1. Выполнить действия над матрицами.

1.

2.

3.

4.

5.

6.

7.

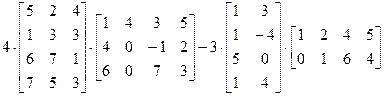
8.

9.

10.

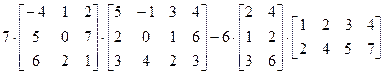
Задание № 2. Найти матрицу, обратную матрице .

1. 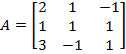.	6.
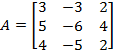
2.	7.
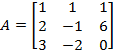
3.	8.
4.	9.
5.	10.