5.1. Линейные (векторные) пространства. С примером линейного, или векторного пространства вы сталкивались еще в школе, изучая в курсе геометрии множество векторов с операциями сложения и умножения на число. Сейчас мы дадим общее определение.
Определение. Пусть 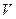 - некоторое множество, в котором определены следующие операции:
- некоторое множество, в котором определены следующие операции:
а) сложения, т.е. 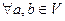
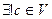 :
: 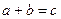 ;
;
б) умножение, т.е. 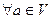
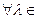 R
R 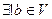 :
: 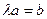 .
.
Будем называть 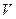 линейным (векторным) пространством, а его элементы – векторами, если выполнены следующие свойства этих операций:
линейным (векторным) пространством, а его элементы – векторами, если выполнены следующие свойства этих операций:
1) 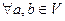
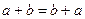 - коммутативность сложения;
- коммутативность сложения;
2) 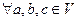
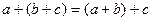 - ассоциативность сложения;
- ассоциативность сложения;
3) 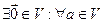
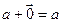 - существование нулевого элемента (чтобы различать нулевой элемент из
- существование нулевого элемента (чтобы различать нулевой элемент из 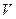 и ноль из R, первый будем обозначать
и ноль из R, первый будем обозначать 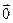 );
);
4) 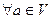
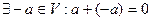 - существование противоположного элемента;
- существование противоположного элемента;
5) 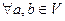
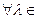 R
R 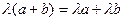 ;
;
6) 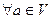
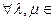 R
R 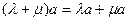 - два свойства дистрибутивности;
- два свойства дистрибутивности;
7) 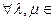 R
R 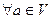
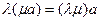 - ассоциативность умножения на число;
- ассоциативность умножения на число;
8) 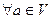
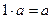 - умножение на
- умножение на 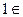 R.
R.
Из этих свойств легко выводятся некоторые следствия.
1) Единственность нулевого элемента в 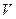 . Действительно, пусть
. Действительно, пусть 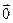 и
и 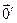 - два нулевых элемента. Тогда
- два нулевых элемента. Тогда 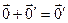 , так как
, так как  - нулевой элемент, с другой стороны,
- нулевой элемент, с другой стороны, 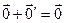 , так как
, так как 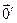 - нулевой элемент. Значит,
- нулевой элемент. Значит, 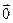 =
=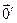 .
.
2) Единственность противоположного элемента 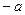 для
для 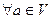 .
.
3) 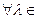 R
R 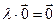 . Действительно,
. Действительно, 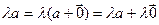 , значит,
, значит, 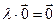 .
.
4) 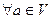
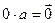 .
.
5) Если 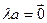 , то выполняется хотя бы одно из равенств
, то выполняется хотя бы одно из равенств 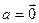 или
или 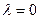 .
.
Доказательства свойств 2,4,5 просты, оставим их в качестве легких упражнений.
Если в определении векторного пространства множество действительных чисел R заменить на множество комплексных чисел С, то получим комплексное векторное пространство. Мы пока будем рассматривать линейные пространства над R, но все, что будет изложено, легко переносится на комплексный случай
Заметим, что определение линейного пространства носит аксиоматический характер: мы ничего не говорим о природе элементов этого пространства, а лишь описываем свойства операций в этом пространстве. Природа же элементов может быть самой различной. Приведем несколько примеров.
а). Первый пример – самый естественный: геометрические векторы с операцией сложения по правилу параллелограмма и умножения на число.
б). Очень важный пример – так называемое арифметическое линейное пространство R n – множество строк длины 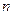 . Его элементами являются наборы из
. Его элементами являются наборы из 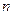 действительных чисел
действительных чисел 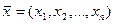 . Операции сложения и умножения на число вводятся покомпонентно, т.е. если
. Операции сложения и умножения на число вводятся покомпонентно, т.е. если 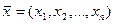 ,
, 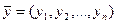 , то
, то 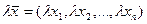
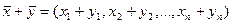 . Аксиомы векторного пространства выполняются – проверьте!
. Аксиомы векторного пространства выполняются – проверьте!
Вместо строк длины 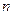 можно рассматривать столбцы высоты
можно рассматривать столбцы высоты 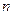 . Очевидно, что по существу это будет то же самое пространство R n, отличается лишь форма записи элементов пространства.
. Очевидно, что по существу это будет то же самое пространство R n, отличается лишь форма записи элементов пространства.
в). Множество всех последовательностей 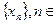 N. Операции сложения и умножения на число задаются покомпонентно: если
N. Операции сложения и умножения на число задаются покомпонентно: если 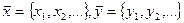 , то
, то
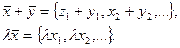
г). Множество всех функций на отрезке 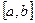 . Операции сложения и умножения на число зададим поточечно:
. Операции сложения и умножения на число зададим поточечно:
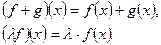
Продумайте сами, что является нулевым элементом в этих примерах, какой элемент является противоположным данному элементу.
Задача. Являются ли данные множества линейными пространствами:
1) множество всех многочленов третьей степени с обычными операциями сложения и умножения на число;
2) множество четных функций на отрезке 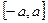 с обычными операциями сложения и умножения на число;
с обычными операциями сложения и умножения на число;
3) множество положительных действительных чисел с операциями: сложение 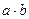 , умножение на число
, умножение на число 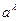 ;
;
4) множество квадратных матриц порядка 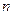 с операциями: сложение
с операциями: сложение 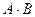 , умножение на число
, умножение на число 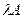 ?
?
Пусть 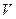 - линейное пространство и
- линейное пространство и 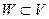 , причем
, причем 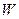 само является линейным пространством (с теми же операциями, что и в
само является линейным пространством (с теми же операциями, что и в 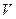 ). Тогда
). Тогда 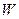 называют подпространством
называют подпространством 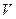 . Так, например, множество векторов, параллельных данной прямой, является подпространством множества всех векторов.
. Так, например, множество векторов, параллельных данной прямой, является подпространством множества всех векторов.
 2014-01-27
2014-01-27 915
915








