Гармонический осциллятор

Казахстан 8 700 973 77 67

Украина 094 947 73 93

Россия 8 985 286 36 67

Линейным одномерным гармоническим осциллятором называют частицу массы 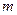, совершающую одномерное движение под действием квазиупругой силы .

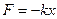Уравнение движения

.

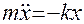Собственная частота классического гармонического осциллятора

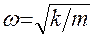, откуда .

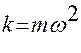Потенциальная энергия осциллятора

.

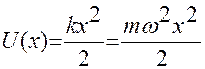Рассмотрение колебательной системы методами квантовой механики: уравнение Шредингера для стационарных состояний частицы в параболической потенциальной яме

.

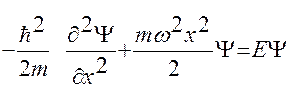Преобразуем это уравнение следующим образом

;

.

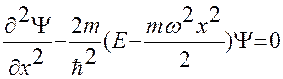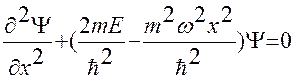Введем обозначения: 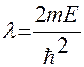и .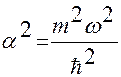

Тогда

.

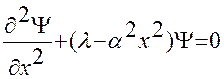Решение этого уравнения должно удовлетворять следующим требованиям:

1) 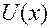симметрична относительно начала координат, следовательно, 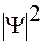должно быть тоже симметрична по отношению к началу координат (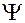- симметрична или асимметрично);

2) при .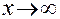

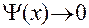Предположим, что 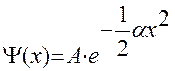- решение уравнения Шредингнра.

Тогда

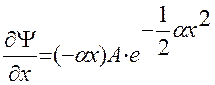и .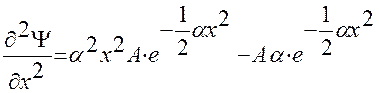

Подставляя решение в уравнение Шредингера, получим

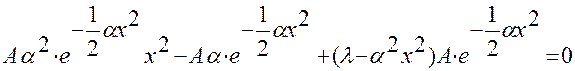
или

.

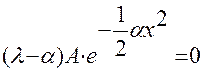Отсюда следует, что искомая функция будет решением при 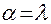. Тогда

.

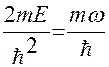Следовательно,

.

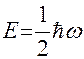Состояние с энергией 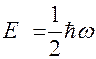- основное квантовое состояние осциллятора.

Возможные значения полной энергии гармонического осциллятора

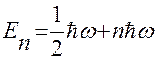или , .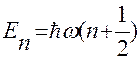

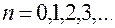Энергетический спектр квантового гармонического осциллятора является дискретным, а уровни энергии 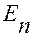- эквидистантны

.

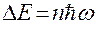Взаимодействие квантового осциллятора с фотоном (излучение или поглощение света) приводит к изменению вида функции: превращает симметричную функцию в антисимметричную, и наоборот. Это приводит к необходимости правила отбора

.

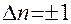Поэтому квантово-механический осциллятор способен поглотить лишь 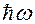и осуществить при этом переход только на соседний уровень.

Из условия нормировки

,

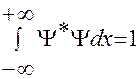тогда .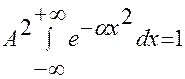

Т.к. функция симметрична относительно начала координат, то

.

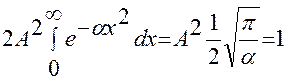Откуда

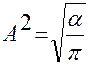или .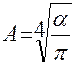

Таким образом

.

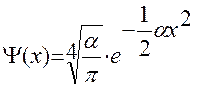Если известен вид функции 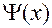, то можно найти все другие величины. Среднее значение координаты:

.

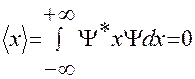Среднее значение проекции импульса

.

.

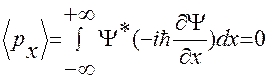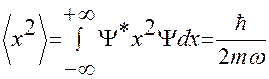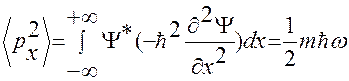
В квазиклассическом приближении

.

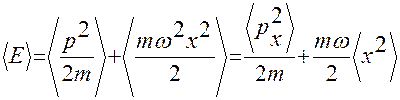Отсюда следует, что средние значения потенциальной и кинетической энергий осциллятора равны:

;

.

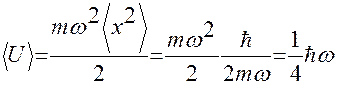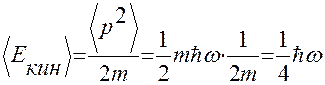Значениям энергии 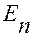соответствуют собственные функции 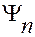. Все функции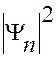должны быть симметричны относительно начала координат Функции 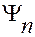- либо симметричны, либо антисимметричны. При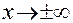 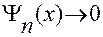. Если все эти функции стремятся к нулю на бесконечности, то они должны содержать множитель 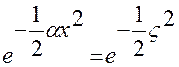(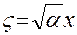). Решение уравнения Шредингера для произвольных 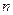имеет вид:

,

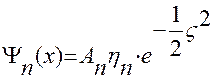где 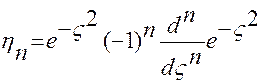- это полином Чебышева-Эрмита, степень которого возрастает с увеличением 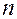; 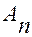- это нормировочный множитель

.

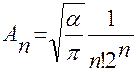Следовательно,

.

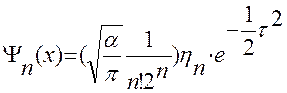Конкретный вид полиномов:

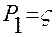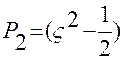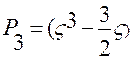; ; и т.д.

Некоторые особенности классических и квантовых осцилляторов.

1. Разрешенные значения 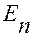для квантово-механического осциллятора представляют собой набор эквидиситантных энергетических уровней, а собственные 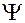- функции – набор стоячих волн, заключенных в потенциальной яме параболической формы.

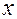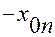Для классического осциллятора границы этой ямы определяют границы пространства, в котором может быть локализована частица. Расстояние по оси от до .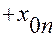

График 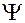- функции, являющейся решением уравнения Шредингера, выходит за рамки ограничивающей кривой 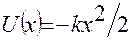. Такое поведение 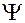- функции связано с тем, что она должна быть непрерывной и гладкой везде, в том числе и в точках поворота, и при этом должно выполняться соотношение неопределенности.

2. Вероятность локализации классического осциллятора в окрестностях точки с координатой 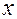в потенциальной яме является наибольшей в точках поворота (где скорость 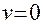), т.е. на стенках параболы.

Для квантово-механического осциллятора 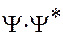имеет конечное значение и на границах ямы и на некотором расстоянии от нее. Следовательно, существует конечная вероятность локализации частицы вне пределов ямы. Наибольшая вероятность локализации частицы - в точках, соответствующих «пучностям» 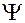- функций.

Для больших 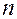функция 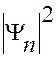имеет распределение, близкое к классическому. В этом проявляется принцип соответствия.