Для вычисления допустимых значений энергии гармонического осциллятора в квантовой механике, необходимо решить задачу на собственные значения оператора энергии 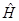 . В классической механике с учётом квадратичной зависимости потенциальной энергии от величины смещения
. В классической механике с учётом квадратичной зависимости потенциальной энергии от величины смещения 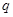 , имеем:
, имеем:
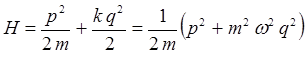
Для упрощения вычислений, полагаем, 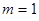 и классический гамильтониан осциллятора тогда берём в виде:
и классический гамильтониан осциллятора тогда берём в виде:
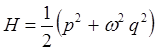
сумму квадратов в полученном выражении удобно представить в виде квадратов модуля комплексной величины:
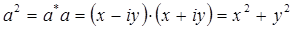
тогда, соответственно будем иметь:
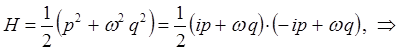
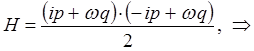
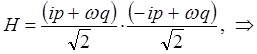
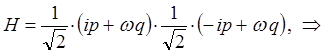
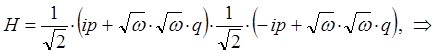
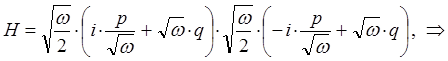
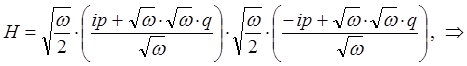
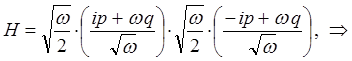
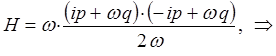
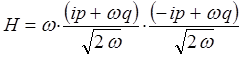
поскольку:
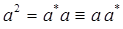
имеем:
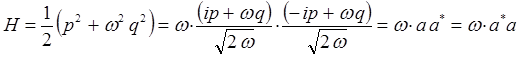
где
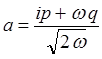
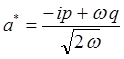
откуда следует, что:
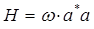
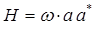
очевидно, что:
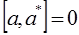
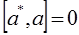
На основании второго постулата квантовой механики имеем:
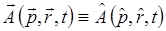
тогда соответственно, выражение:
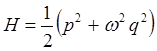
можно будет представить далее к виду:
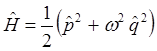
где
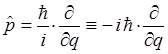
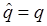
переходя к атомным единицам измерения (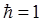 ), перепишем соответствующее выражение для оператора импульса в виде:
), перепишем соответствующее выражение для оператора импульса в виде:
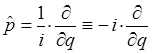
На основании приведенных выше выкладок, строим выражение для оператора Гамильтона, аналогичное:
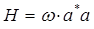
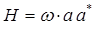
имеем таким образом:
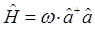
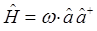
учитывая свойство коммутативности для операторов импульса и координаты:
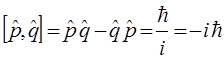
или в атомных единицах измерения по Хартри:
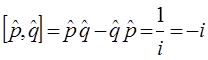
Учитывая приведенные выше выкладки, будем иметь соответственно:
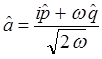
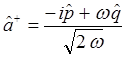
поэтому:
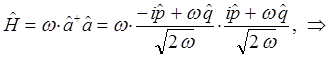
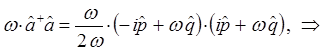
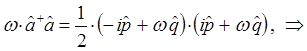
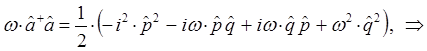
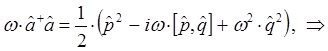
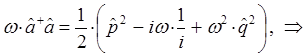
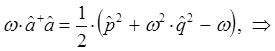
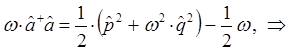
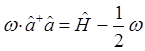
Таким образом, мы пришли к выражению вида:
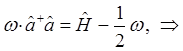
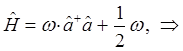
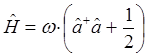
Сравнение выражений для оператора Гамильтона, даёт:
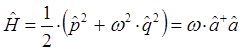
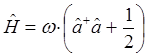
где дополнительный член вида 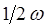 - типично квантовая поправка. Аналогично из второй эквивалентной формы для Гамильтониана вида:
- типично квантовая поправка. Аналогично из второй эквивалентной формы для Гамильтониана вида:
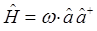
находим соответственно, что:
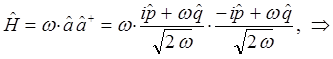
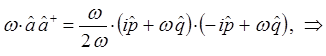
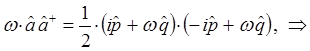
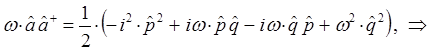
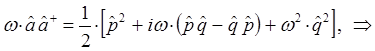
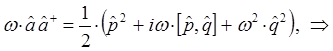
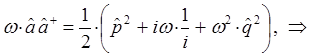
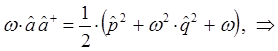
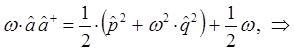
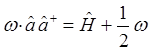
Таким образом, в ходе проделанных выкладок, приходим к выражению вида:
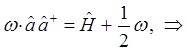
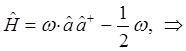
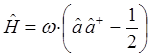
имеем соответственно:
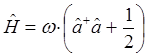
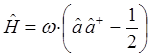
Теперь установим ряд вспомогательных соотношений. Для этих целей, вычислим произведение операторов 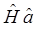 и
и 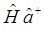 , используя полученные уже ранее выражения вида:
, используя полученные уже ранее выражения вида:
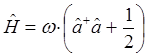
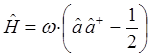
имеем таким образом:
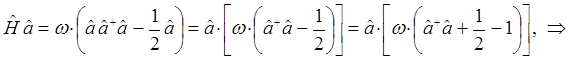
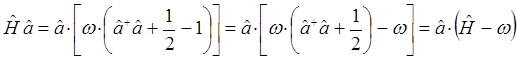
и аналогично:
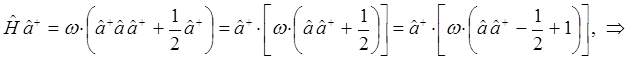
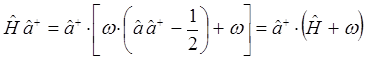
Таким образом, мы получили соотношения вида:
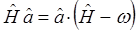
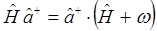
Далее процедура отыскания всех допустимых значений энергии квантового осциллятора состоит в получении эквидистантного спектра. Для этого необходимо решить задачу на собственные значения оператора:
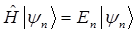
которая легко решается с помощью полученных нами уже выше выражений:
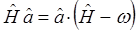
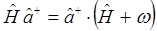
Действительно, пусть 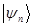 является собственным вектором, удовлетворяющим выражению вида:
является собственным вектором, удовлетворяющим выражению вида:
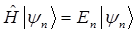
тогда вектора 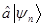 и
и 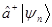 также будут являться собственными векторами этой задачи и произведение операторов
также будут являться собственными векторами этой задачи и произведение операторов 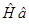 и
и 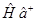 при действии на вектор
при действии на вектор 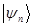 , также будут давать собственные вектора. После соответствующих подстановок, имеем:
, также будут давать собственные вектора. После соответствующих подстановок, имеем:
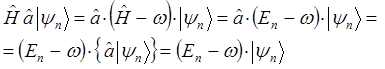
и аналогично:
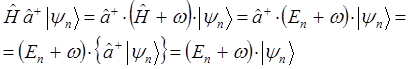
имеем соответственно:
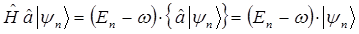
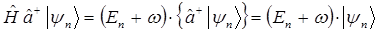
Следовательно, действие оператора 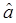 на вектор
на вектор 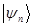 приводит к состоянию с энергией на
приводит к состоянию с энергией на 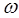 меньше, а действие оператора
меньше, а действие оператора 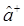 на вектор
на вектор 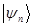 - к состоянию с энергией, на
- к состоянию с энергией, на 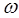 больше (в атомных единицах Хартри, где
больше (в атомных единицах Хартри, где 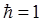 ), т.е. зная
), т.е. зная 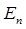 , мы знаем и все остальные энергии. На основании приведенных выше выкладок, построим цепочку собственных векторов и соответствующих им энергий.
, мы знаем и все остальные энергии. На основании приведенных выше выкладок, построим цепочку собственных векторов и соответствующих им энергий.
| Состояние | Энергия |
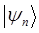 | 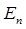 |
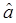 | 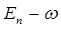 |
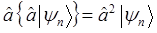 | 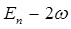 |
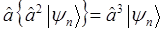 | 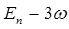 |
 |  |
Эта цепочка не может быть бесконечной, поскольку 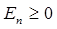 , т.е. все допустимые энергии должны быть положительными величинами. Поэтому в данной цепочке, очевидно, должно существовать некоторое предельное состояние
, т.е. все допустимые энергии должны быть положительными величинами. Поэтому в данной цепочке, очевидно, должно существовать некоторое предельное состояние 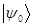 , причём такое, что на нём цепочка будет обрываться:
, причём такое, что на нём цепочка будет обрываться:
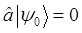
Соответствующая данному состоянию 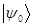 энергия
энергия 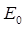 - наименьшая из возможных, т.е. отвечает основному состоянию осциллятора, характеризуя энергию так называемых нулевых колебаний:
- наименьшая из возможных, т.е. отвечает основному состоянию осциллятора, характеризуя энергию так называемых нулевых колебаний:
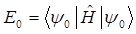
поскольку:
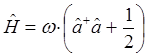
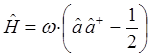
тогда соответственно:
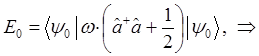
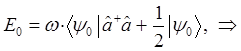
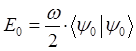
учитывая, что:
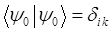
где
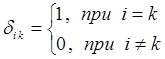
имеем окончательно:
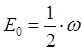
| Состояние | Энергия |
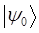 | 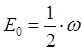 |
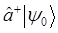 | 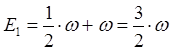 |
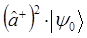 | 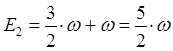 |
 |  |
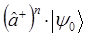 | 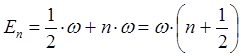 |
Очевидно, все выше лежащие состояния 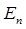 >
> 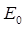 будут являться возбуждёнными. Возбуждённые состояния получают из
будут являться возбуждёнными. Возбуждённые состояния получают из 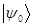 с помощью выражений вида:
с помощью выражений вида:
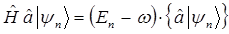
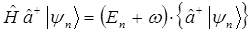
Этот процесс перехода от n -го состояния к 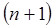 - му, уже ничем не ограничен, здесь
- му, уже ничем не ограничен, здесь 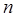 принимает любое целое значение
принимает любое целое значение 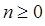 . Явный вид волновых функций легко устанавливается, если известно состояние
. Явный вид волновых функций легко устанавливается, если известно состояние 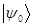 , соответствующее энергии нулевых колебаний и находится из уравнения вида:
, соответствующее энергии нулевых колебаний и находится из уравнения вида:
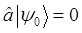
поскольку:
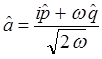
тогда соответственно операторное уравнение:
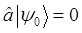
преобразуется к виду:
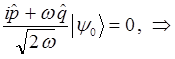
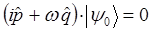
учитывая, что:
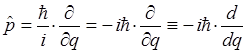
или в атомных единицах Хартри, где 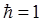 :
:
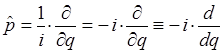
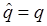
тогда соответственно будем иметь:
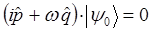
учитывая, что:
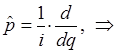
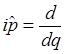
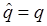
поэтому:
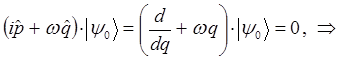
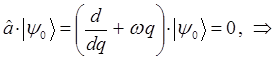
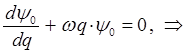
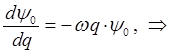
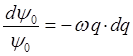
Интегрируя правую и левую части полученного дифференциального уравнения, приходим к выражению:
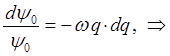
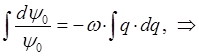
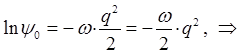
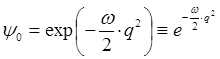
учитывая, что:
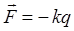
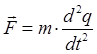
имеем для случая классического (гармонического) осциллятора:
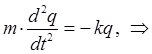
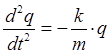
полагая:
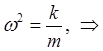
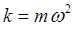
имеем:
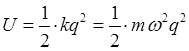
Учитывая приведенные выше соображения, не трудно записать выражение для Гамильтониана в операторной и координатной формах:
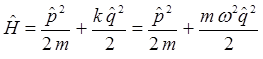
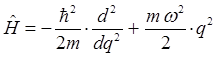
поскольку:
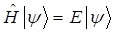
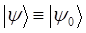
тогда:
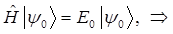
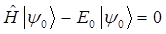
Подставляя функцию вида:
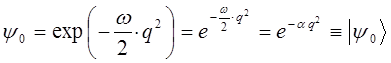
в уравнение:
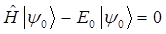
где как было показано выше:
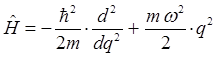
будем иметь соответственно:
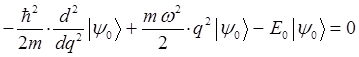
с учётом выражения:
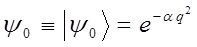
имеем:
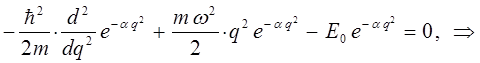
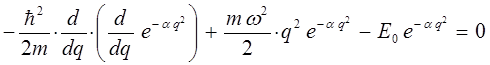
Для упрощения дальнейших выкладок, вычислим отдельно выражение:
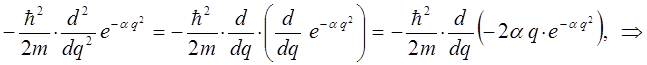
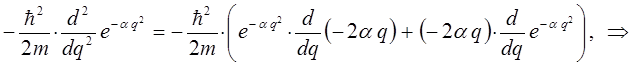
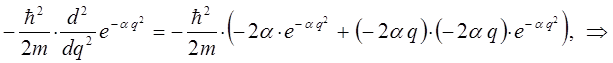
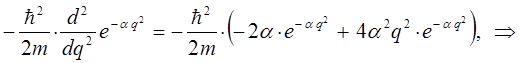
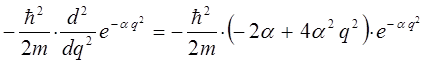
Полученное выражение подставим теперь в соответствующее операторное уравнение вида:
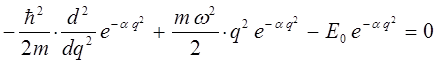
имеем:
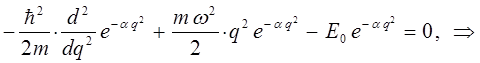
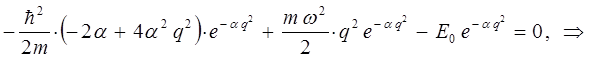
поскольку:
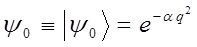
имеем:
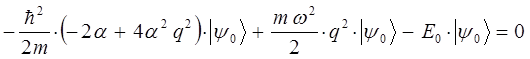
Сокращая полученное выражение на общий член 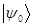 , получим тождество вида:
, получим тождество вида:
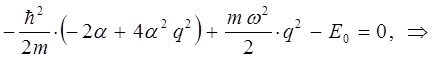
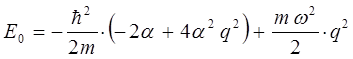
Преобразовывая полученное выражение далее, будем иметь соответственно:
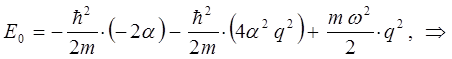

Поскольку коэффициенты при одинаковых степенях по-определению обращаются в нуль:
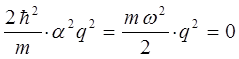
и выражение определяющее энергию нулевых колебаний квантового осциллятора 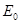 будет иметь вид:
будет иметь вид:
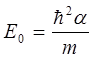
для нахождения коэффициента 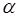 , входящего в выражение для энергии нулевых колебаний
, входящего в выражение для энергии нулевых колебаний 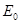 , воспользуемся вторым и третьим членами исходного уравнения для энергии нулевых колебаний квантового осциллятора:
, воспользуемся вторым и третьим членами исходного уравнения для энергии нулевых колебаний квантового осциллятора:

имеем:
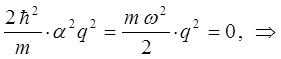
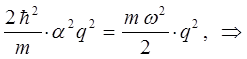
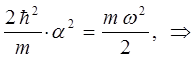
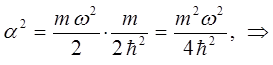
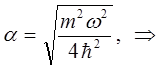
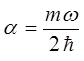
тогда после подстановки полученного выражения в найденное выше уравнение для энергии нулевых колебаний, будем иметь соответственно:
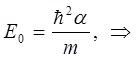
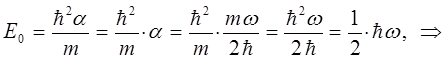
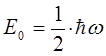
с учётом приведенных выше выкладок, записанное ранее выражение для энергии 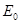 может быть уточнено и записано в виде:
может быть уточнено и записано в виде:
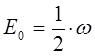
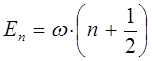
и аналогично:
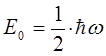
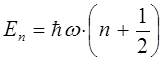
учитывая, что:
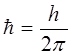
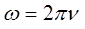
будем иметь соответственно:
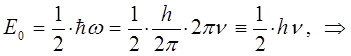
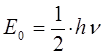
и аналогично получаем:
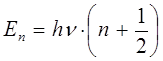
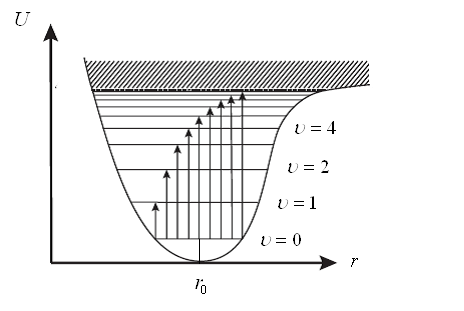
Рис.14. Ангармонизм колебаний осциллятора
Спектр квантового осциллятора, описываемый уравнениями вида:
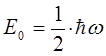
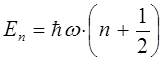
или
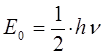
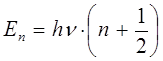
называется эквидистантным или равноотстоящим. Необходимо отметить, что наименьшая энергия 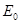 начинается с ненулевого значения:
начинается с ненулевого значения:
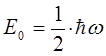
тогда как в классической механике 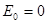 (состояние покоя
(состояние покоя 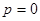 и
и 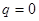 ). Таким образом, квантовый осциллятор, в отличие от своего классического аналога, никогда не находится в состоянии покоя. Даже в состоянии с наименьшей энергией
). Таким образом, квантовый осциллятор, в отличие от своего классического аналога, никогда не находится в состоянии покоя. Даже в состоянии с наименьшей энергией 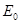 частица колеблется (что находится в полном соответствии с принципом неопределённости Гейзенберга):
частица колеблется (что находится в полном соответствии с принципом неопределённости Гейзенберга):
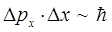
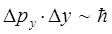
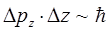
если бы такого не происходило (отсутствовала энергия нулевых колебаний 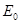 ), тогда в силу вступали бы законы классической механики, т.е. существовала бы возможность одновременного измерения двух физических величин – координаты и импульса частицы. Существование ненулевого значения энергии
), тогда в силу вступали бы законы классической механики, т.е. существовала бы возможность одновременного измерения двух физических величин – координаты и импульса частицы. Существование ненулевого значения энергии 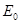 находит своё отражение в физических явлениях, возникающих при низких температурах (в том числе и при
находит своё отражение в физических явлениях, возникающих при низких температурах (в том числе и при 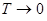 ). Так, рассеяние света кристаллами обусловлено колебаниями атомов кристаллической решётки. При понижении температуры, амплитуда колебаний понижается, однако сами колебания как показали экспериментальные данные, не прекращаются и вблизи абсолютного нуля. Это в свою очередь приводит к соответствующему рассеянию света. Другой важный пример – нулевые колебания вакуума. Так, электромагнитное поле описывается набором осцилляторов, представляющих колебания векторов напряжённости электрического
). Так, рассеяние света кристаллами обусловлено колебаниями атомов кристаллической решётки. При понижении температуры, амплитуда колебаний понижается, однако сами колебания как показали экспериментальные данные, не прекращаются и вблизи абсолютного нуля. Это в свою очередь приводит к соответствующему рассеянию света. Другой важный пример – нулевые колебания вакуума. Так, электромагнитное поле описывается набором осцилляторов, представляющих колебания векторов напряжённости электрического 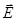 и магнитного
и магнитного 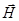 поля. Квантование осцилляторов поля позволяет правильно интерпретировать основное его состояние – вакуум. Так, в вакууме
поля. Квантование осцилляторов поля позволяет правильно интерпретировать основное его состояние – вакуум. Так, в вакууме 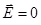 , но из-за нулевых колебаний электромагнитное поле флуктуирует, т.е.
, но из-за нулевых колебаний электромагнитное поле флуктуирует, т.е. 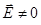 . Это, в свою очередь, приводит к флуктуациям координаты электрона в атомах и молекулах, а, следовательно, к смещению всех энергетических уровней (так называемый лэмбовский сдвиг). Хотя сам сдвиг и незначителен (например, в атоме кислорода
. Это, в свою очередь, приводит к флуктуациям координаты электрона в атомах и молекулах, а, следовательно, к смещению всех энергетических уровней (так называемый лэмбовский сдвиг). Хотя сам сдвиг и незначителен (например, в атоме кислорода 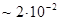 эВ), он имеет принципиальное значение, подтверждая таким образом, существование наличия нулевых колебаний и таким образом основные концепции квантовой механики. Ещё одной особенностью энергетических уровней квантового осциллятора является их эквидистантность. Это означает, что расстояние между двумя соседними уровнями является постоянной для данного осциллятора величиной. Для доказательства справедливости данного утверждения, найдём разность энергий двух соседних энергетических уровней:
эВ), он имеет принципиальное значение, подтверждая таким образом, существование наличия нулевых колебаний и таким образом основные концепции квантовой механики. Ещё одной особенностью энергетических уровней квантового осциллятора является их эквидистантность. Это означает, что расстояние между двумя соседними уровнями является постоянной для данного осциллятора величиной. Для доказательства справедливости данного утверждения, найдём разность энергий двух соседних энергетических уровней:
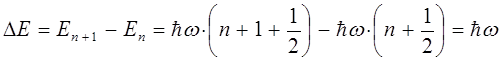
Следовательно, разность энергий между двумя соседними энергетическими уровнями 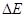 не зависит от колебательного квантового числа
не зависит от колебательного квантового числа 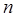 , энергетические уровни находятся на одинаковом расстоянии друг от друга. При этом переход осциллятора из возбуждённого состояния
, энергетические уровни находятся на одинаковом расстоянии друг от друга. При этом переход осциллятора из возбуждённого состояния 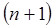 в основное
в основное 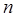 , сопровождается излучением кванта энергии
, сопровождается излучением кванта энергии 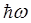 . Выражение для
. Выражение для 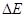 можно также переписать в другой, эквивалентной приведенной выше форме:
можно также переписать в другой, эквивалентной приведенной выше форме:
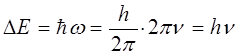
 2015-03-22
2015-03-22 1392
1392
