Линейный гармонический осциллятор

в квантовой механике.

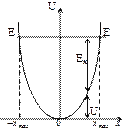
Линейный гармонический осциллятор – это система, совершающая одномерное движение под действием квазиупругой силы. Он является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора равна: 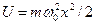, (5.1)

где 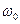— собственная частота колебаний осциллятора, т — масса частицы.

Рассмотрим сначала поведение классического гармонического осциллятора. Пусть частица с полной энергией 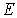совершает колебания в силовом поле (4.77) (рис.4.24). Точк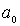и и 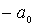, в которых полная энергия частицы равна потенциальной энергии 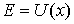, являются для частицы точками поворота. Частица совершает колебательные движения между стенками потенциальной ямы внутри отрезка 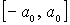, выйти за пределы которого она не может. Амплитуда колебаний 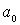определяется выражением .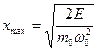

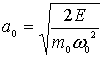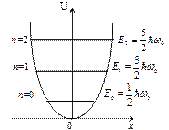
Зависимость (5.1) имеет вид параболы (рис. 5.1), т.е. «потенциальная яма» в данном случае является параболической. Амплитуда малых колебаний классического осциллятора определяется его полной энергией Е. В точках с координатами ±х_max полная энергия Е равна потенциальной энергии. Поэтому с классической точки зрения частица не может выйти за пределы области (– х_max, + х_max).

Гармонический осциллятор в квантовой механике – квантовый осциллятор – опи­сывается уравнением Шредингера (4.2), учитывающим выражение (5.1) для потенциальной энергии. Тогда стационарные состояния квантового осциллятора определяются уравнением Шредингера вида

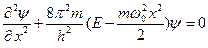(5.2)

где Е — полная энергия осциллятора. В теории дифференциальных уравнений до­казывается, что уравнение (5.2) решается только при собственных значениях энергии

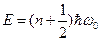(5.3)

где 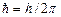. Формула (5.3)показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т.е. квантуется.

Это соотношение и определяет закон квантования энергии гармонического осциллятора. Отметим, что энергетические уровни гармонического осциллятора, в отличие, например, от случая прямоугольной потенциальной ямы, являются эквидистантными, т.е. расположены на одинаковом энергетическом расстоянии 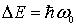друг от друга

Энергия ограничена снизу отличным от нуля минималь­ным значением энергии 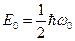. Существование минимальной энергии, назы­ваемой энергией нулевых колебаний, пред­ставляет собой прямое следствие соотношения неопределенностей.

Поместим начало координат в точку, являющуюся положением равновесия гармонического осциллятора, совершающего колебания по закону 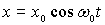. Тогда неопределенность координаты 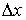принимает вид

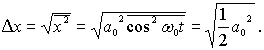
Амплитуда колебаний 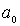связана с энергией 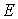соотношением 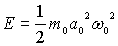, следовательно

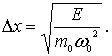
Аналогично, для неопределенности импульса имеем

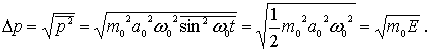
Подставляя 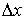и 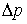в соотношение неопределенностей 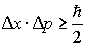, получаем следующее условие

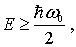
т.е. действительно, минимальное значение энергии гармонического осциллятора есть .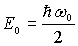

Нулевые колебания играют в физике весьма важную роль, в частности они обусловливают отсутствие кристаллизации жидкого гелия при нормальном давлении даже при абсолютном нуле температур. Велика роль нулевых колебаний и в объяснении природы сил молекулярных взаимодействий, физических особенностей поверхностного натяжения, адсорбции и других молекулярных явлений. На эксперименте наличие нулевых колебаний наблюдается, в частности, в опытах по рассеянию света кристаллами при низких температурах.

Наличие нулевых колебаний означает, что частица не может находиться на дне «потенциальной ямы», причем этот вывод не зависит от ее формы. В самом деле, «падение на дно ямы» связано с обращением в нуль импульса частицы, а вместе с темиего неопределенности. Тогда неопределенность координаты становится сколь угодно большой, что противоречит, в свою очередь, пребыванию частицы в «потенциальной яме».

Вывод о наличии энергии нулевых колебаний квантового осциллятора противоре­чит выводам классической теории. Например, классическая физика приводит к выводу, что при Т=0 К (Е_к=0) энергия колебательного движения атомов кристалла должна обращаться в нуль. Однако эксперименты по рассеянию света показывают, что при Т®0 колебания атомов в кристалле не прекращаются.

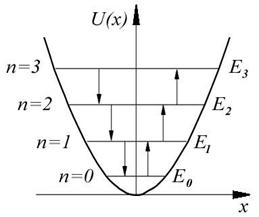
Из формулы (5.3) также следует, что уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга (рис. 5.2), а имен­но расстояние между соседними энергетическими уровнями равно 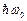, причем мини­мальное значение энергии ½ .

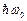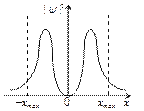Квантово-механический расчет показывает, что частицу можно обнаружить за пределами дозволенной области (– х_max, + х_max), в то время как с классической точки зрения она не может выйти за ее пределы. Следовательно, имеется отличная от нуля вероят­ность обнаружить частицу в той области, которая является классически запрещенной. Этот результат (без вывода) демонстрируется на рис.5.3, где приводится квантовая плотность вероятности 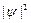обнаружения осциллятора для состояния п =1. Из рисунка следует, что для квантового осциллятора действительно плотность вероятности имеет конечные значения за пределами классически дозволенной области |x|³ х_max, т.е. имеется конечная (но небольшая) вероятность обнаружить частицу за пределами «потенциальной ямы».

44. Атом водорода по теории Шредингера

Уравнение Шредингера позволяет решить вопрос о строении водородоподобного атома, т. е. атома, который состоит из положительно заряженного ядра с зарядом +Ze и одного электрона. Потенциальная энергия взаимодействия электрона с ядром, согласно формуле (2.14), равна:

где Z - порядковый номер элемента в таблице Менделеева (для атома водорода = 1);
e - заряд электрона;
r - расстояние между электроном и ядром: 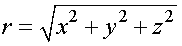(см. формулу (1.1));
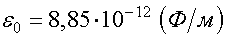- электрическая постоянная.

Если подставить (5.17) в уравнение Шредингера (5.16), то окажется, что это уравнение имеет решение не при всех отрицательных значениях электрона E, а только таких, которые удовлетворяют условию:

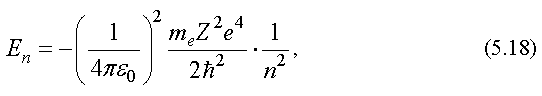
где n = 1, 2, 3,... - целое число.

Заметим, что формула (5.18) совпадает с формулой (5.11), полученной в теории Бора.

Из формулы (5.18) следует, что энергия электрона в атоме квантуется.

Найденная при этих значениях энергии волновая функция Ψ зависит от трех квантовых чисел:

n - главное квантовое число, n = 1, 2, 3,...;
l - орбитальное квантовое число, l = 1, 2, 3,..., (n -1);
m_L - магнитное квантовое число, m_L = - l, - l +1,..., 0,..., (l -1), l.

Волновая функция определяет состояние электрона в атоме, а квадрат ее модуля - вероятность обнаружения электрона в единице объема (см. (5.14)).

Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы "размазан" по всему объему, образуя электронное облако. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число m_L характеризует ориентацию электронного облака в пространстве.

В квантовой физике, по аналогии с спектроскопией, состояние электрона, характеризующееся квантовым числом l = 0, называется S - состоянием, l = 1 - p - состоянием, l = 2 - d - состоянием и т. д. Для обозначения различных состояний электрона в атоме используют следующие обозначения: значения главного квантового числа указывают перед условным обозначением орбитального квантового числа. Например, электроны в состояниях n = 1, l = 0 обозначаются 1 S, при n = 2, l = 1 обозначаются 2 p и т. д.

Квантовые числа позволяют компактно описать закономерности в спектре испускания (поглощения) атома водорода.

46. Штерна-Герлаха опыт

опыт, экспериментально подтвердивший, что атомы обладают магнитным моментом, проекция которогона направление внешнего магнитного поля принимает лишь определённые значения (пространственноквантована). Осуществлен в 1922 О. Штерном и немецким физиком В. Герлахом (W. Gerlach), которыеисследовали прохождение пучка атомов Ag (а затем и др. элементов) в сильно неоднородном магнитномполе (см. рис.) с целью проверки теоретически полученной формулы пространств. квантования проекции μ_zна направление Z магнитного момента атома μ_o: μ_z = μ_o m (т = 0±1,...).

На атом, обладающий магнитным моментом и движущийся в неоднородном вдоль Z магнитном поле Н,действует сила F= μ_z дН/дZ, которая отклоняет его от первоначального направления движения. Еслипроекция магнитного момента атома могла бы изменяться непрерывно, то на пластинке П наблюдалась быразмытая широкая полоса. Однако в Ш.— Г. о. было обнаружено расщепление пучка атомов на 2компоненты, симметрично смещенные относительно первичного направления распространения на величинуΔ — на пластинке появлялись две узкие полосы. Это указывало на то, что проекция магнитного моментаатома μ_z на направление поля Н принимает только два отличающиеся знаком значения ±μ_o, т. е. μ_oориентируется вдоль Н и в противоположном направлении. Величина магнитного момента атома μ_о,измеренная в опыте по смещению Δ, оказалась равной Бора магнетону.

Ш.—Г. о. сыграл большую роль в дальнейшем развитии представлений об электроне. Согласноквантовой теории Бора — Зоммерфельда, орбитальный и, следовательно, магнитный моментыиспользуемых в опыте атомов с одним электроном во внешней оболочке равны нулю, поэтому такие атомыне должны были бы вообще отклоняться магнитным полем. Ш.—Г. о., показавший, что эти атомы вопрекитеории обладают магнитным моментом, а также другие более ранние эксперименты привели в 1925 Дж. Ю.Уленбека и С. Гаудсмита к гипотезе существования собственного механического момента электрона —Спина.

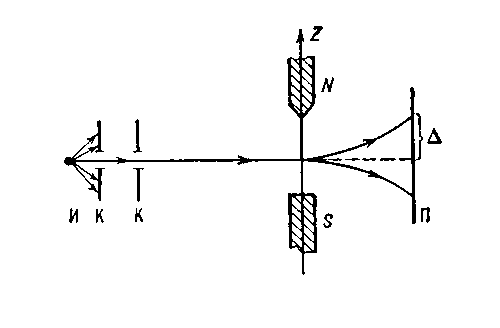
Схема опыта Штерна-Герлаха: И — источник атомов; К — щели, формирующие узкий пучок; N, S —полюса магнита, создающего постоянное неоднородное поле; П — пластинка, на которую оседают атомы; ∆— величина отклонения пучка от первоначального направления. Опыт производится в вакууме.