План
1. Введение.
2. Движение заряженных частиц в однородном электрическом поле.
3. Понятие об электронной оптике.
4. Движение заряженных частиц в однородном магнитном поле.
5. Эффект Холла.
6. Принцип действия ускорителя заряженных частиц.
1. Введение. Воздействуя на потоки электронов и ионов электрическими и магнитными полями, можно управлять этими потоками, изменять их интенсивность и направление движения. Такая возможность лежит в основе действия различных важных электронных приборов (осциллографов, электронных микроскопов, телевизионных трубок и др.)
Концентрированный поток электронов используется для обработки металлов (электроннолучевая обработка).
2. Движение заряженных частиц в однородном электрическом поле.
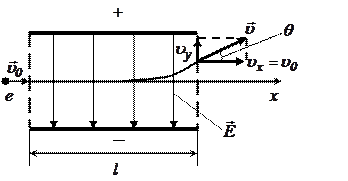 | Предположим, что заряженная частица массой 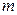 с зарядом с зарядом 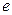 движется первоначально вдоль оси X со скоростью движется первоначально вдоль оси X со скоростью 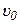 , попадает в электрическое поле плоского конденсатора (рис. 26.1) длинной , попадает в электрическое поле плоского конденсатора (рис. 26.1) длинной 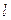 . Считаем поле . Считаем поле 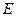 однородным. Найдем угол однородным. Найдем угол 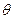 отклонения частицы в электрическом поле от первоначального направления. Уравнения движения: отклонения частицы в электрическом поле от первоначального направления. Уравнения движения: |
| Рис. 26.1 |
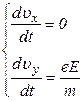 .
.
Интегрируя 1-ое и 2-ое уравнения:
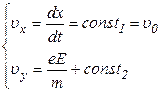 ,
,
где 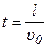 - время нахождения частицы в электрическом поле.
- время нахождения частицы в электрическом поле.
При 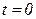
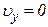 , следовательно
, следовательно 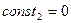 , то есть
, то есть 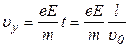 , тогда тангенс угла отклонения
, тогда тангенс угла отклонения 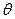 :
:
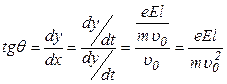 ,
,
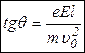
То есть отклонение частицы зависит от отношения 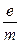 - удельного заряда частицы, величины поля, длины конденсатора (прямо пропорционально этим величинам) и от квадрата начальной скорости (обратно пропорционально).
- удельного заряда частицы, величины поля, длины конденсатора (прямо пропорционально этим величинам) и от квадрата начальной скорости (обратно пропорционально).
3. Понятие об электронной оптике. Если пластины конденсатора сделать из металлических сеток, то в зависимости от направления и скорости движения электронов, величины поля и параметров конденсатора можно управлять электронными потоками подобно оптическим элементам. Например, явления отражения и преломления показаны на рис. 26.2.
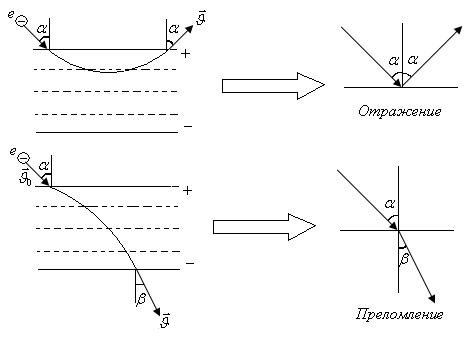 | ||||||||
| Рис. 26.2 |
Электрическая линза (рис.26.3).
Электрическая линза состоит из двух коаксиальных цилиндров, потенциалы которых 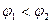 . Электроны, испущенные из точки
. Электроны, испущенные из точки 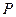 в левой половине «линзы» вблизи границы цилиндров отклоняется к оси цилиндров (вдоль силовых линий, обозначенных пунктиром), в правой половине линзы от оси, но там электроны уже набрали скорость и пучок электронов, хотя и уменьшает сходимость, все же остается сходящимся. В правой части рисунка изображен оптический аналог собирающей линзы.
в левой половине «линзы» вблизи границы цилиндров отклоняется к оси цилиндров (вдоль силовых линий, обозначенных пунктиром), в правой половине линзы от оси, но там электроны уже набрали скорость и пучок электронов, хотя и уменьшает сходимость, все же остается сходящимся. В правой части рисунка изображен оптический аналог собирающей линзы.
 |
| Рис. 26.3 |
4. Движение заряженных частиц в однородном магнитном поле.
|
|
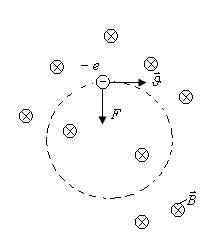 Пусть имеется однородное магнитное поле, например поле соленоида. Предположим, что частица с зарядом
Пусть имеется однородное магнитное поле, например поле соленоида. Предположим, что частица с зарядом 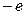 (электрон), обладающая начальной скоростью
(электрон), обладающая начальной скоростью 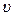 , попадает в магнитное поле с индукцией
, попадает в магнитное поле с индукцией 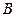 . Будем считать поле однородным, направленным перпендикулярно к скорости
. Будем считать поле однородным, направленным перпендикулярно к скорости 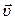 . На частицу действует магнитная сила (магнитная составляющая силы Лоренца)
. На частицу действует магнитная сила (магнитная составляющая силы Лоренца) 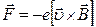 (рис.26.4). Эта сила, будучи направлена перпендикулярно направлению движения, является центростремительно силой. А движение под действием центростремительной силы есть движение по окружности. Радиус окружности
(рис.26.4). Эта сила, будучи направлена перпендикулярно направлению движения, является центростремительно силой. А движение под действием центростремительной силы есть движение по окружности. Радиус окружности 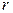 определяется условием
определяется условием 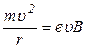 , откуда:
, откуда: 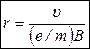
И называется циклотронный (ларморовский) радиус. Он прямо пропорционален скорости, обратно пропорционален удельному заряду 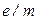 и магнитной индукции.
и магнитной индукции.
Энергия электрона может быть набрана в электрическом поле 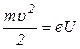 , где
, где 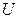 - ускоряющая напряженность, тогда
- ускоряющая напряженность, тогда 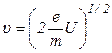 и циклотронный радиус:
и циклотронный радиус:
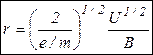
Если начальная скорость частицы составляет некоторый угол 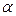 с направлением поля, то частица движется по спирали (рис.26.5).
с направлением поля, то частица движется по спирали (рис.26.5).
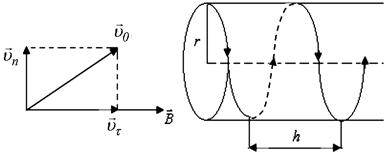 | Шаг витка спирали 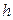 определяется тангенциальной составляющей скорости частицы определяется тангенциальной составляющей скорости частицы 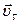 и периодом и периодом 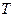 (который зависит от нормальной составляющей скорости (который зависит от нормальной составляющей скорости 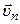 ). ). 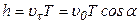 . . |
| Рис. 26.5 |
Период обращения:
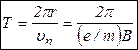
Тогда:
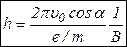
Циклическая (циклотронная частота обращения электрона):
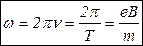
 2014-01-27
2014-01-27 1347
1347