Следствие2.
Обозначим:
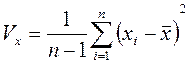 ,
,
вариация данных по 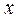 ,
,
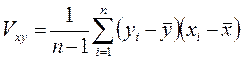 ,
,
ковариация данных по 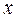 и
и 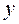 , тогда
, тогда
|
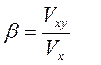
Вычисление матрицы ковариации с использованием метода ведущего фактора опирается на ряд гипотез.
|
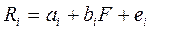 ,
,
где F - некоторая случайная величина;
ai bi - за терминированные числа;
|
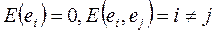
Замечание1. В силу (77) случайная величина F - называется ведущим фактором. Равенство (78) показывает, что все случайные колебания эффективности Ri определяются ведущим фактором F, а случайные отклонения от прямой взаимно некоррелированны и имеют нулевые математические ожидания.
Определение1. Взвешенная, с учетом капитала эмитента, сумма эффективностей всех рисковых ценных бумаг, продающихся на данном рынке (бирже), называют эффективностью данного рынка (бирже).
Рассмотрим какой-либо рынок и обозначим через Rрынка - эффективность этого рынка.
Гипотеза2. Ведущим фактором для эффективностей всех ценных бумаг, продающихся на данном рынке является эффективностью данного рынка, то есть F = Rрынка.
|
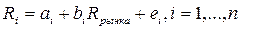
Из (79) следует,
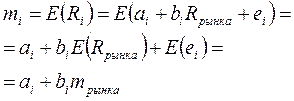
Итак,
|
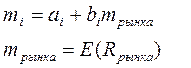 .
.
|
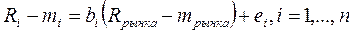
Откуда, получаем
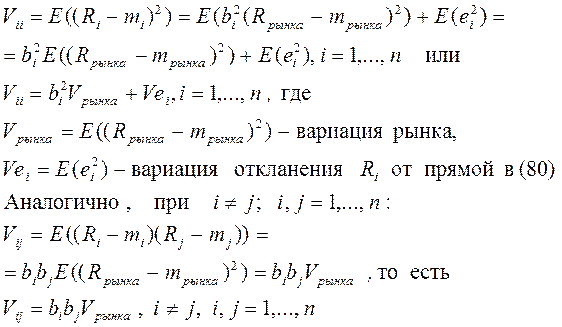
При выборе (82) и (83) учтена независимость случайных величин:
Алгоритм расчета.
1. Рассчитывается эффективность ценных бумаг 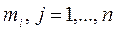 , продающихся на данном рынке, по формулам (2), с учетом информации за последние 5 лет. Промежуток между покупкой и продажей, при этом, берется равным 1 кварталу, чтобы учесть дивиденды.
, продающихся на данном рынке, по формулам (2), с учетом информации за последние 5 лет. Промежуток между покупкой и продажей, при этом, берется равным 1 кварталу, чтобы учесть дивиденды.
2. Рассчитывается эффективность всего рынка ценных бумаг 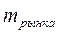 , суммированием эффективностей
, суммированием эффективностей 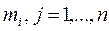 с учетов капиталов, соответствующих эмитентов.
с учетов капиталов, соответствующих эмитентов.
3. Используя (81) и метод наименьших квадратов, определяются коэффициенты 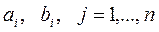 .
.
4. Рассчитывается 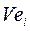 , как значение целевой функции в методе наименьших квадратов (см. п.3), при оптимальных
, как значение целевой функции в методе наименьших квадратов (см. п.3), при оптимальных 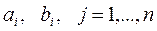 .
.
5. По формулам (82) и (83) рассчитываются элементы матрицы ковариации.
Пусть на рынке наряду с рискованными ценными бумагами продается и безрисковая ценная бумага с эффективностью 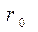 . В этом случае вместо
. В этом случае вместо 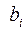 используют
используют 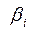 (бета вклада) и рассчитывают величину:
(бета вклада) и рассчитывают величину:
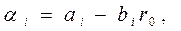
называемую "альфа вклада".
Для каждой ценной бумаги, входящей в индекс SP500 в США регулярно публикуются соответствующие альфа, бета, "приспособленные бета" (линейно зависит от бета), а также величин
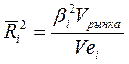 ,
,
характеризующих долю рынка для данной ценной бумаги, вносимую риском рынка в целом.
 2014-01-28
2014-01-28 711
711








