Метод прямого статистического анализа используется на практике только для оценки эффективности ценных бумаг, а матрица ковариации считается с использованием других методов, например, с использованием метода ведущих факторов.
Метод ведущих факторов основан на методе наименьших квадратов. Рассмотрим простейший вариант метода наименьших квадратов, в случае, когда ведущий фактор один, уравнение регрессии – линейное.
Имеется n – данных неизвестной функциональной зависимости между x и y
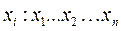
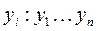
Построим линейную функцию:
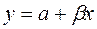 ,
,
которая наименее откланяется от табличных данных.
Таким образом, задача заключается в том, чтобы найти такие параметры a и b при которых прямая менее всего отклоняется от всех точек одновременно.
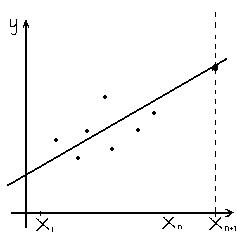 |
Рис.1.Геометрическая интерпретация метода наименьших квадратов.
Математически это приводим к следующей задачи минимизации:
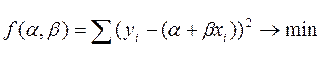
Минимум достигается там, где градиент функции f равен нулю.
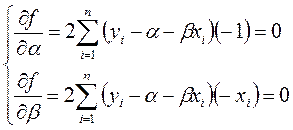
Преобразуем первое уравнение:
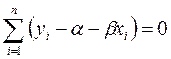
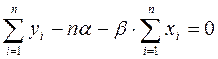
Окончательно
|
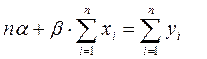
Преобразуем второе уравнение
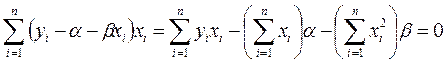
Окончательно
|
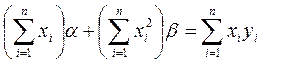
Получим два уравнения (74), (75) для двух неизвестных (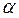 и
и 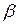 ).
).
Расчеты удобно проводить с помощью таблицы, записывая вместо *, рассчитанные величины:
| … | n | 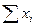
| 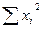
| 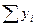
| 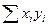
| |||
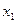
| 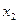
| 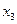
| … | 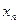
| * | - | - | - |
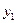
| 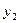
| 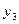
| … | 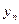
| - | - | * | - |
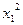
| 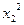
| 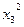
| … | 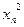
| - | * | - | - |
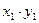
| … | … | … | 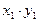
| - | - | - | * |
Из уравнения (1) и (2) следует, что
|
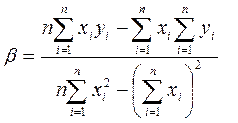
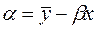 ,
,
где
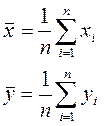
Запишем формулу (76) в более удобной форме.
Лемма1. Для любых n, xi, yi, i=1,…,n справедливо тождество:
|
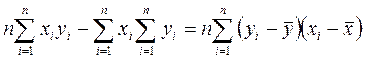
Доказательство:
Обозначим 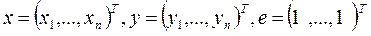 и запишем
и запишем 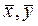 и сумму в правой части (77) с использованием евклидового скалярного произведения:
и сумму в правой части (77) с использованием евклидового скалярного произведения:
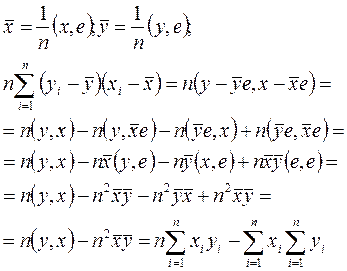 ,
,
что и требовалось доказать.
Лемма доказана.
Положим в (77) 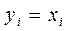 получим, что справедливо следующее.
получим, что справедливо следующее.
Следствие1. Для любых 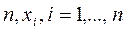 справедливо тождество:
справедливо тождество:
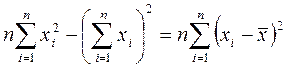
 2014-01-28
2014-01-28 840
840








