Задача №1.1
Модуль 1
ЗАДАЧА №1.1-5
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
«ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра «Автомобили и тракторы»
по дисциплине «Теория автомобиля и трактора» для студентов специальности 190201.65 «Автомобиле- и тракторостроение»
Выполнил: студент гр.АТ-09-2
Мокренко А.В.
Проверил: проф.
Куприянов М.П.
Липецк 2012г
Определить характеристики воздействия на трактор или автомобиль при движении по данному микропрофилю со скоростью 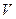 , причём воздействие стационарное и эргодическое. Форму профиля задать самостоятельно.
, причём воздействие стационарное и эргодическое. Форму профиля задать самостоятельно.
Таблица 1.1
| № варианта | ||||||||||
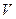 , м/с , м/с
| 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 |
| № варианта | ||||||||||
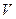 , м/с , м/с
| 5,5 | 6,0 | 6,5 | 7,0 | 7,5 | 8,0 | 8,5 | 9,0 | 9,5 | 10,0 |
Выполнение этого задания следует производить в следующей последовательности. Получив у преподавателя номер варианта, необходимо самостоятельно задать форму микропрофиля пути в виде профилограммы.

Пусть самостоятельно была выбрана профилограмма, изображённая на рисунке 1.
Для оценки характера воздействий при движении машины по заданному микропрофилю используют следующие характеристики:
1) математическое ожидание;
2) дисперсия;
3) корреляционная функция;
4) спектральная плотность (энергетический спектр).
Математическое ожидание определяется по формуле:
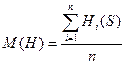 .
.
Определение высоты микронеровностей 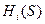 будем производить через
будем производить через
каждые четыре метра поверхности пути. Таких точек получается 9, т.е. 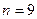 . Тогда математическое ожидание будет равно
. Тогда математическое ожидание будет равно
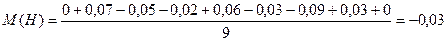
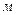 .
.
Величина дисперсии может быть определена по формуле:
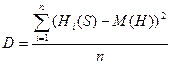 .
.
Высоту микронеровностей будем определять так же, как и при расчёте математического ожидания. Тогда
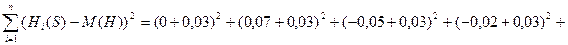
 .
.
Дисперсия 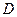 в этом случае
в этом случае
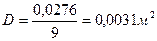 .
.
Корреляционную функцию 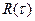 определяют по микропрофилю пути при движении по нему с заданной скоростью
определяют по микропрофилю пути при движении по нему с заданной скоростью 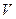 . Так как корреляционная функция отражает характер неровностей микропрофиля пути и скорость движения по нему, то, следовательно, она отражает характер воздействия на машину при её движении по данному микропрофилю. Для определения корреляционной функции профилограмму
. Так как корреляционная функция отражает характер неровностей микропрофиля пути и скорость движения по нему, то, следовательно, она отражает характер воздействия на машину при её движении по данному микропрофилю. Для определения корреляционной функции профилограмму 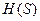 , изображённую на рисунке 1 перестраивают в график зависимости
, изображённую на рисунке 1 перестраивают в график зависимости 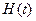 , используя соотношение
, используя соотношение 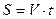 .
.
Пусть заданная скорость  . Задаваясь, например, значением времени
. Задаваясь, например, значением времени  , определим величину
, определим величину  и по профилограмме (рис.1) найдём величину
и по профилограмме (рис.1) найдём величину 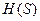 , соответствующую этому значению
, соответствующую этому значению 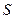 . Найденное значение будет величиной
. Найденное значение будет величиной 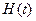 при
при  . Аналогично задаваясь другим значением времени
. Аналогично задаваясь другим значением времени 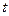 , определяем
, определяем 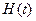 . В результате такого расчёта получим зависимость характера воздействия на машину при её движении по данному микропрофилю со скоростью
. В результате такого расчёта получим зависимость характера воздействия на машину при её движении по данному микропрофилю со скоростью  , изображённую на рисунке 2.
, изображённую на рисунке 2.

Корреляционная функция определяется по формуле:
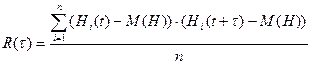 ,
,
где 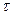 - разность моментов времени наблюдения ординаты случайной функции
- разность моментов времени наблюдения ординаты случайной функции 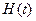 ;
; 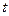 - текущее значение времени;
- текущее значение времени; 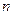 - число выбранных точек для определения корреляционной функции при выбранном значении
- число выбранных точек для определения корреляционной функции при выбранном значении 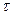 .
.
Определим значения корреляционной функции при различных значениях величины 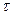 .
.
При 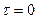
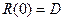 , т.к.
, т.к. 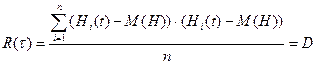 .
.
При разности моментов времени наблюдения 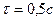 количество точек может быть бесчисленное множество, т.к. важным является только то, чтобы ординаты
количество точек может быть бесчисленное множество, т.к. важным является только то, чтобы ординаты 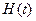 отстояли друг от друга на величину
отстояли друг от друга на величину 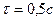 по числовой оси
по числовой оси 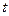 . Чем больше взятых точек, тем точнее будет определено значение корреляционной функции. Возьмём для примера 6 точек (
. Чем больше взятых точек, тем точнее будет определено значение корреляционной функции. Возьмём для примера 6 точек (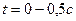 ;
; 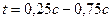 ;
; 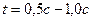 ;
; 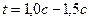 ;
; 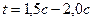 ;
; 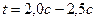 ). Тогда значение корреляционной функции при
). Тогда значение корреляционной функции при 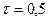 будет
будет
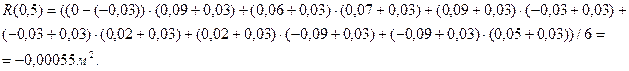 При
При 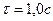 аналогично выбираем точки на числовой оси
аналогично выбираем точки на числовой оси 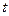 , отстоящие друг от друга на
, отстоящие друг от друга на 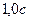 . Таких точек также может быть бесчисленное множество. Возьмём для примера 5 точек (
. Таких точек также может быть бесчисленное множество. Возьмём для примера 5 точек (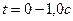 ;
; 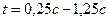 ;
; 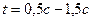 ;
; 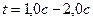 ;
; 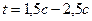 ). Тогда
). Тогда
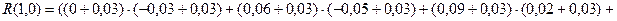
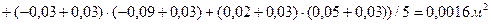 .
.
При 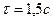
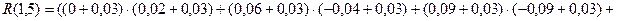
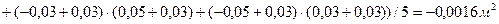 .
.
При 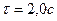
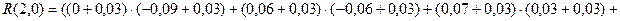
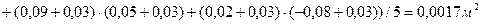 .
.
По данным, полученным в результате расчёта, строится зависимость 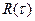 , которая характеризует воздействия на машину при её движении по заданному микропрофилю со скоростью
, которая характеризует воздействия на машину при её движении по заданному микропрофилю со скоростью  . Построенная корреляционная функция изображена на рисунке 3.
. Построенная корреляционная функция изображена на рисунке 3.
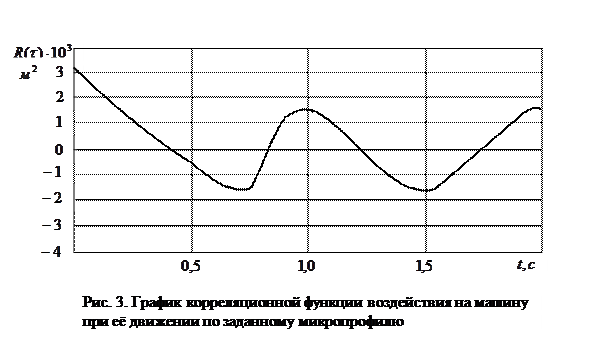
Анализируя зависимость 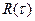 можно сделать вывод, что характер воздействия при движении машины по заданному микропрофилю представляет собой процесс с малой степенью случайности и высокой периодичностью, т.е. процесс, близкий к обычному гармоническому процессу.
можно сделать вывод, что характер воздействия при движении машины по заданному микропрофилю представляет собой процесс с малой степенью случайности и высокой периодичностью, т.е. процесс, близкий к обычному гармоническому процессу.
Построив график корреляционной функции, можно подобрать аналитическое выражение функции 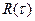 .
.
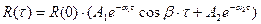 ,
,
где 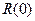 - дисперсия высоты неровностей;
- дисперсия высоты неровностей; 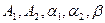 - коэффициенты, которые рассчитываются по графику корреляционной функции или выбираются из таблицы 1. 2 в зависимости от типа почвенного фона.
- коэффициенты, которые рассчитываются по графику корреляционной функции или выбираются из таблицы 1. 2 в зависимости от типа почвенного фона.
Таблица 1.2
| Фон |
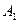
|
 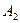
|
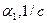
|
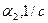
| 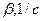
|
| Асфальтовая дорога | 0,85 | 0,15 | 0,20 | 0,05 | 0,60 |
| Булыжная дорога | 1,00 | - | 0,45 | - | - |
| Грунтовая дорога | - | 1,00 | - | 0,58 | 0,63 |
| Стерня пшеницы | - | 1,00 | - | 0,45 | 0,29 |
| Слежавшаяся пахота | 0,70 | 0,30 | 0,65 | 3,20 | 1,57 |
Коэффициенты 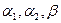 зависят от скорости движения. В таблице 1.2 приведены их значения при движении со скоростью 1м/с. Значения этих коэффициентов для другой скорости движения определяют по их значениям для скорости
зависят от скорости движения. В таблице 1.2 приведены их значения при движении со скоростью 1м/с. Значения этих коэффициентов для другой скорости движения определяют по их значениям для скорости 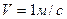 , пользуясь соотношениями
, пользуясь соотношениями
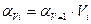 ;
; 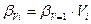 .
.
Так при скорости движения по почвенному фону – слежавшаяся пахота  коэффициенты равны
коэффициенты равны 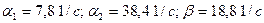 . Для аналитического выражения корреляционной функции
. Для аналитического выражения корреляционной функции 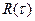 , приведённого выше, можно определить спектральную плотность, которая будет иметь следующий вид:
, приведённого выше, можно определить спектральную плотность, которая будет иметь следующий вид:
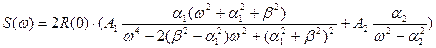 ,
,
где 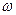 - текущая частота процесса воздействия на машину при движении её по микропрофилю.
- текущая частота процесса воздействия на машину при движении её по микропрофилю.
Зная значения коэффициентов 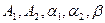 и задаваясь различными значениями текущей частоты процесса воздействия
и задаваясь различными значениями текущей частоты процесса воздействия 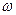 , определяем значения спектральной плотности
, определяем значения спектральной плотности 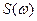 . Например, определим значение
. Например, определим значение 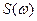 при
при 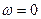 .
.
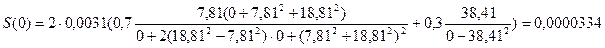 .
.
Величина спектральной плотности 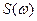 измеряется в
измеряется в 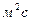 .
.
Задавая другие значения текущей частоты процесса воздействия 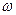 , и делая соответствующие вычисления, получим:
, и делая соответствующие вычисления, получим:
при 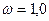
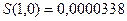 ;
;
при 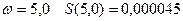 ;
;
при 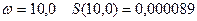 ;
;
при 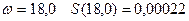 ;
;
при 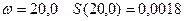 ;
;
при 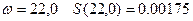 ;
;
при 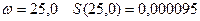 ;
;
при 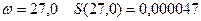 ;
;
при 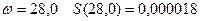 .
.
По полученным значениям строим график спектральной плотности, вид которого изображён на рисунке 4. Анализ этого графика позволяет сделать следующий вывод. Так как спектральная плотность 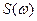 характеризует непрерывный спектр имеющихся частот в полученной случайной функции
характеризует непрерывный спектр имеющихся частот в полученной случайной функции 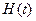 воздействия на машину при её движении по заданному микропрофилю со скоростью
воздействия на машину при её движении по заданному микропрофилю со скоростью  , то судя по графику, она имеет один резко выраженный максимум при текущей частоте процесса воздействия
, то судя по графику, она имеет один резко выраженный максимум при текущей частоте процесса воздействия 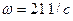 . Иными словами полученная случайная функция воздействия
. Иными словами полученная случайная функция воздействия 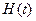 содержит в основном частоты, близкие к одной частоте, соответствующей максимуму спектральной плотности
содержит в основном частоты, близкие к одной частоте, соответствующей максимуму спектральной плотности 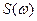 . Такой характер воздействия легко воспроизвести при проведении испытаний машин.
. Такой характер воздействия легко воспроизвести при проведении испытаний машин.

Нуклеїнові кислоти були відкриті швейцарським вченим Мішером у 1869 р. в ядрах лейкоцитів. У зв’язку з цим їх назвали нуклеїновими від nucleus – ядро.
Нуклеїнові кислоти, це біополімери з молекулярною масою 2,5´104 – 1,2´108, мономерами яких є нуклеотиди. Існує два типи нуклеїнових кислот: рибонуклеїнова (РНК) та дезоксирибонуклеїнова (ДНК) кислоти.
Нуклеотид – це сполука, що складається із залишків азотистої основи, пентози та фосфорної кислоти.
1. В якості пентози до складу РНК входить рибоза, до ДНК – дезоксирибоза.
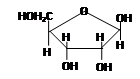 | 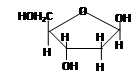 | ||||||
|
|
 2014-01-31
2014-01-31 767
767








