Определение степени подвижности пространственной кинематической цепи
Пусть мы имеем n звеньев, из которых собирается кинематическая цепь. Пока звенья не соединены в кинематические пары, каждое из них имеет шесть степеней свободы (степеней подвижности). Все звенья до соединения в кинематическую цепь следовательно имели 6n степеней подвижности. После сборки звеньев в кинематическую цепь мы получим кинематические пары различных классов (с разными степенями подвижности). Предположим, что наша кинематическая цепь имеет кинематические пары всех пяти классов.
Примем следующие обозначения:
Р5 - количество кинематических пар пятого класса в образованной нами кинематической цепи,
Р4 - количество кинематических пар четвёртого класса,
Р3 - количество кинематических пар третьего класса,
Р2 - количество кинематических пар второго класса,
Р1 - количество кинематических пар первого класса.
Каждая кинематическая пара ограничивает перемещение звеньев, отбирает у них столько степеней свободы, как её класс. Каждая кинематическая пара 5 класса отбирает у звеньев 5 степеней свободы. Все пары пятого класса отнимут у звеньев 5Р5 степеней свободы, четвёртого класса - 4Р4, третьего - 3Р3, второго - 2Р2, первого - 1Р1. Если из общего количества степеней свободы звеньев 6n вычесть все потерянные степени свободы, получим число степеней подвижности кинематической цепи W:
W = 6n - 5P5 - 4Р4 - 3Р3 - 2Р2 - 1P1. (1)
Степенью подвижности механизма называется количество независимых координат, которые необходимо задать для определения положений звеньев механизма в системе координат, жестко связанной со стойкой.
Механизм отличается от кинематической цепи тем, что у него одно звено полностью закреплено. Закрепленное звено потеряло все шесть степеней свободы. Следовательно в механизме число подвижных звеньев равно n-1. Подставив в формулу (1) количество подвижных звеньев n-1, получим формулу для определения степени подвижности механизма:
W = 6(n-1) - 5P5 - 4Р4 - 3Р3 - 2Р2 - 1P1. (2)
Формула (2) впервые была получена Малышевым для пространственных механизмов.
Рассмотрим формулу Малышева для определения степени подвижности плоских механизмов. Все звенья плоского механизма могут иметь три степени подвижности, а кинематические пары соответственно могут иметь 1 или 2 степени подвижности. Если плоские кинематические пары рассматривать по классам, то они могут быть только пятого и четвёртого классов. При этом необходимо учесть, что общее количество степеней подвижности всех звеньев плоского механизма равно 3(n-1). Пары пятого класса теряют две степени подвижности, четвёртого –одну. Таким образом степень подвижности плоского механизма может быть определена по формуле:
W = 3(n-1) - 2P5 - Р4. (3)
Формула (3) для определения степени подвижности плоского механизма впервые была получена Чебышевым П. Л.
В зависимости от числа общих условий связей, накладываемых на механизм, механизмы подразделяют на семейства.
Семейства механизмов и их структурные формулы приведены в таблице 1.
Таблица 2.1 Структурные формулы различных семейств механизмов
| Семейство | Структурная формула | Примечание |
| I II III IV | W=6(n-1)-5P5-4Р4-3Р3-2Р2-1P1 W=5(n-1)-4P5-3Р4-2Р3-Р2 W=4(n-1)-3P5-2Р4-Р3 W=3(n-1)-2P5-Р4 W=2(n-1)- P5 | Сомова-Малышева Чебышева Добровольского |
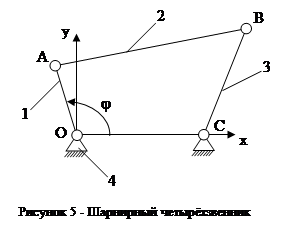
Рассмотрим применение структурной формулы Чебышева П. Л. на конкретном примере. На рисунке 5 изображен шарнирный четырёхзвенник.
1е - звено - кривошип - совершает вращательное движение вокруг оси О (полный оборот);
2е - звено АВ - шатун - совершает плоско - параллельное движение;
3е - звено ВС - коромысло (или балансир) - совершает возвратно- вращательное движение вокруг оси С (неполный оборот);
4е - звено ОС - стойка (станина) - неподвижное звено.
Количество звеньев n = 4. Кинематические пары: 4-1, 1-2, 2-3, 3-4. Имеем 4 одноподвижные пары 5го класса. Относительное движение всех звеньев плоское. Механизм плоский. Определяем степень подвижности его по формуле Чебышева П. Л.:
W = 3(n-1) - 2P5 - Р4 = 3(4-1) - 2 × 4 - 0 = 1.
Механизм имеет степень подвижности равную 1. Это значит, что достаточно задать одну координату любому звену механизма в системе координат, жестко связанной со станиной, чтобы определить положения всех остальных звеньев. Например, в нашем случае достаточно задаться углом поворота кривошипа j1.
Пассивные связи и избыточные звенья
Звенья и кинематические пары, которые не влияют на характер движения механизма в целом, называются избыточными (лишними) звеньями и парами, а обусловленные ими связи называются пассивными связями.
При определении степени подвижности механизма избыточные звенья и кинематические пары не должны учитываться.
В сложных стержневых механизмах не всегда на глаз можно определить степень подвижности. В этих случаях необходимо воспользоваться формулой Чебышева.

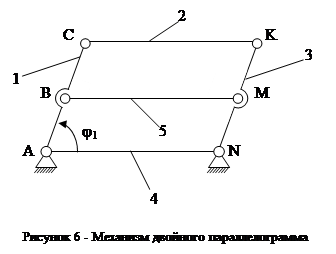
Определим W механизма двойного параллелограмма (рисунок 6). Здесь АВ = ВС = КМ = MN; AN || BM || CK; AN = BM = CK и AС || KN. При таком соотношении звеньев механизм имеет W=1, т. е. достаточно задать положение звена 1 углом j1, чтобы определить положения всех остальных звеньев. Если зафиксировать звено 1 в любом положении, то остальные звенья будут неподвижны. Определим W по формуле Чебышева. Количество звеньев – n=5, кинематических пар 5го класса Р5=6, количество кинематических пар четвёртого класса - Р4=0.
W = 3(n-1) - 2P5 - Р4 = 3(5-1) - 2 × 6 - 0 = 0.
Если W=0, то должен быть не механизм, а жесткая ферма. Мы видим, что механизм может осуществлять движение. Если в этом механизме мысленно убрать звено 5 (или 2), то при этом характер движения остальных звеньев останется неизменным. Механизм превращается в обычный четырёхзвенник, W которого мы уже определили – W=1. При устранении звена 5 одновременно устраняется 2 кинематические пары: 5-1, 5-3. Следовательно, в этом механизме избыточными является одно звено и две кинематические пары.
Рассмотрим ещё один пример - механизм Маркуса, часто применяющийся в качестве привода качающегося конвейера (рисунок 7). Количество звеньев n = 6. Кинематические пары: 6-1, 1-2, 2-3, 2-4, 3-4, 3-6, 4-5, 5-6 все пятого класса Р5 = 8, Р4 = 0.
Определим W по формуле Чебышева:
W = 3(n-1) - 2P5 - Р4 = 3(6-1) - 2 × 8 - 0 = -1.
По схеме механизма видно, что он будет работать и W=1.
Пусть отсутствует непосредственное соединение звеньев 2-3. Звенья 3, 4, 5 всё равно займут положение, соответствующее углу поворота j1 звена 1, т. к. звенья 1, 2, 4 должны быть зафиксированы этим углом. То же самое можно получить, если удалить кинематическую пару 2-4 или 4-3. Здесь одна кинематическая пара избыточная. Её можно не учитывать. Тогда:
W = 3(6-1) - 2 × 7 = 1.
При этом замечаем, что устранение звена влечёт за собой устранение некоторых кинематических пар. Устранение кинематических пар (прекращение контакта звеньев) не влечёт за собой как неизбежное устранение входящих в неё звеньев.
Соединение звеньев, где соединяется 3 и более звеньев, называется узлом. В узле на одну кинематическую пару меньше, чем звеньев.
Избыточные кинематические пары и звенья накладывают дополнительные условия на точность изготовления механизма, однако несмотря на это в механизм вводят иногда пассивное звено или лишнюю связь с целью получения каких либо дополнительных необходимых качеств; увеличение прочности, уменьшение трения и др.
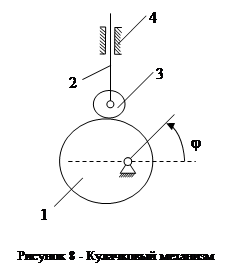
Определим W кулачкового механизма, изображенного на рисунке 2.8. Здесь звенья 1- кулачок, 2- толкатель, 3- ролик, 4- стойка. Количество звеньев n=4. Кинематические пары 1-4, 2-4, 2-3 пятого класса и 3-1 – высшая плоская кинематическая пара 4го класса. При повороте кулачка на угол j толкатель займёт определённое положение. На первый взгляд W=1.
Определим W по формуле Чебышева:
W = 3(4-1) - 2 × 3 - 2 = 2.
Здесь есть лишняя степень подвижности. Если бы ролик неподвижно закрепить с толкателем, то W механизма была бы равна единице. Поворот ролика по отношению к остальным звеньям не оказывает никакого влияния. Угол поворота ролика- это и есть лишняя степень свободы механизма.
Лишней степенью свободы называется такая степень свободы в движении некоторых звеньев, устранение которой не вызывает изменений в характере движения других звеньев по кинематическим соображениям.
При этом имеется в виду абсолютное или относительное движение звена. Устранение лишней степени свободы не влечёт за собой устранение звена.
Прежде чем пользоваться формулой Чебышева необходимо мысленно исключать из рассмотрения пассивные связи и лишние степени свободы.
Формула Чебышева в общем случае даёт правильный ответ. В общих случаях пассивные связи и лишние степени свободы не существуют и могут быть только в частных случаях.
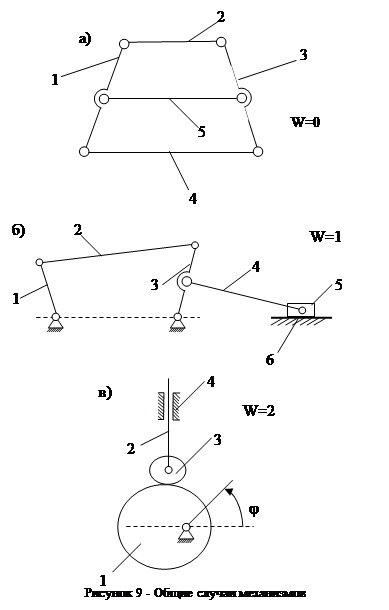
Например: механизм двойного параллелограмма является частным случаем такого же механизма, когда звенья не параллельны (рисунок 9а); механизм Маркуса является частным случаем механизма, когда оси шарнирных соединений звеньев 2, 4 не совпадают (рисунок 9б); круглый ролик является более частным случаем геометрической формы ролика не круглой формы (рисунок 9в).
Таким образом формула Чебышева даёт возможность выявить характерные особенности (частности) механизмов.
 2014-01-31
2014-01-31 14493
14493
