Структурный синтез механизмов

Целью структурного синтеза механизма является его структурно-кинематическая схема с минимальным количеством звеньев для преобразования движения заданного количества входных звеньев в тре­буемое движение выходных звеньев. Задачи структурного синтеза многовариантны. Одно и то же преобразование движения можно получить различными по структуре механизмами. При выборе оптимальной структурно-кинематической схемы учитывается технология изготовления звеньев и кинематических пар, требования по точности изготовления и монтажа механизма, условияего эксплуатации.

Синтез структурно-кинематаческих схем механизмов может осуществляться:

- методом наслоения структурных групп;

-методом инверсии;

- методом конструктивного преобразования.

Метод наслоения структурных групп заключается в том, что к основному двухзвенному механизму, состоящему из входного звена и стойки, присоединяются структурные группы с нулевой подвижностью.

В зависимости от того, какими кинематическими парами они присое­диняются, какова форма звеньевмогут получиться разные варианты механизмов.

Рассмотрим пример.

Присоединением к основному механизму, состоящему из входного звена 2 и стойки 1, группы Ассура П класса 1-го вида (звенья 3,4 и кинематические пары B,C,D) получим кривошипно-коромысловый механизм (рис.2.5.).

Если к этому же основному механизму присоединить группу Ассура П класса 2-го вида, то получим кривошипно-ползунный механизм (рис.2.6.)

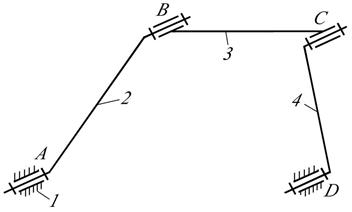
Рис. 2.5

Присоединяя к полученному механизму еще одну такуюже струк­турную группу, получим схему V-образного двигателя внутреннего сгорания (рис.2.7.).

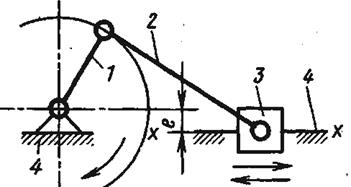
Рис.2.6.

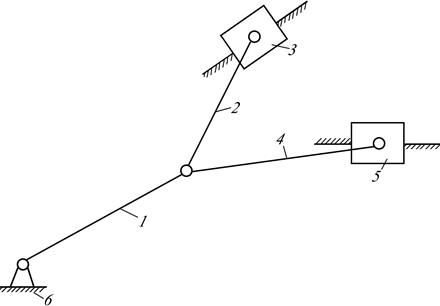
Рис. 2.7.

М етод инверсии заключается в получении различных вариантов механизма путем замены функций одного звена функциями другого звена. Например: инверсией кривошипно-ползунного механизма ( рис.2.8а) можнополучить кривошипно-кулисный механизм (рис.2.8б), если стойкой сделать звено 1, а выходным – звено 2.

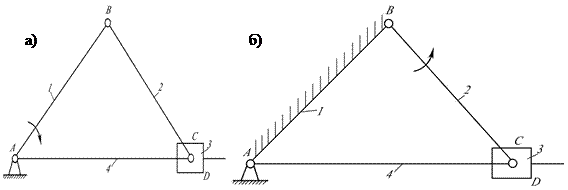Рис.2.8.

Всё выше сказанное относится к плоским статически определимым (т.е. идеальным)механизмам. В идеальном механизме отсутствуют избыточные связи. Однако, вследствие неточности изготовления, идеальный плоскиймеханизм становится, в некоторой степени, пространственным,поэтому при структурном анализе механизма целесообразно использовать формулу Сомова-Малышева, подставляя в нее подвижность идеального механизма и выявляя количество избыточных связей.

Рассмотрим пример.

При проектировании кривошипно-ползунного механизма взята структурная схема, состоящаяиз исходного механизма (1,4) и 2-х поводковой группы (2,3) с кинематическими парами 5 класса (рис.2.9). Подвижность этого механизма по формулеЧебышева

W = 3 n – p ₄ – 2 p ₅ = 3 × 3 – 0 – 2 × 4 = 1

Если теперь принять,что, из-за неточностей изготовления этот механизм пространственный,то по формуле Сомова-Малышева найдем число избыточных связей:

g = W – 6(k – 1) + I × p _i = 1 – 6(4 – 1) + 5 × 4 = 3

Избыточные связи не меняют степени подвижности механизма, но при его работе могут вызвать деформация звеньев. Как устранять избыточные связи? Это можно сделать повышая подвижность кинематических пар.

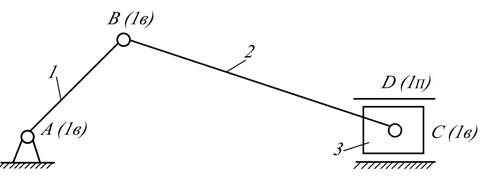
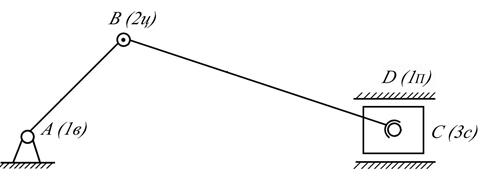
Рис. 2.9

Заменим одноподвижную вращательную кинематическую пару В на 2-х подвижную цилиндрическую, а одноподвижную кинематическую пару С на 3-х подвижную сферическую.

В преобразованном механизме число избыточных связей равно нулю:

g = 1 – 6 × 3 + 5 × 2 +4 × 1 + 3 ×1 = 0

Рассмотрим еще один пример.

Плоский 4-хзвенный механизм с одноподвижными вращательными кинематическими парами (рис.2.10а) с учетом неточностей изготовления (напри­мер, вследствие не параллельности осей A и D) оказывается пространственным. Сборка кинематических цепей 4, 3, 2 и отдельно 1, 4 не вызывает трудностей. Однако, соединить звенья I и 2 в кинематичес­кой паре В (одноподвижная вращательная) можно будет только путем угловых деформаций звеньев.

Определим число избыточных связей по формуле Сомова-Малышева:

g = 1 – 6 × 3 + 5 × 4 = 3

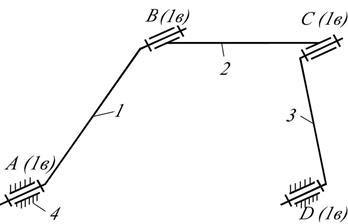а

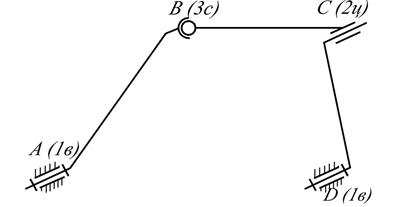
б

Рис. 2.10

т.е. в данной схеме имеется 3 избыточные связи. Устраним эти связи заменяя одноподвижную вращательную кинематическую пару С на двухподвижную цилиндрическую, а одноподвижную вращательную пару В на 3-х подвижную сферическую. Это делаетвозможным без деформаций соединить звенья 2 и 1, т.к. звено 2 получило возможность перемещаться вдоль оси цилиндрического шарнира (рис. 2.10 б).

Структурный синтез может быть произведен так же путем конструктивного преобразования механизма (изменения соотношений размеров, формы, расположения звеньев). Это приводит к качественно иным техни­ческим решениям при сохранении струк­турной схемы или вида механизма.

На рис. 2.11 на сх. а - е представлено конструктивное преобразование кривошипно-ползунного механизма, на сх. ж — н - кривошипно-кулисного механизма, на сх. о, п — синусного механизма, на сх. р, с — тангенсного механизма, на сх. т, у — механизма пантографа.

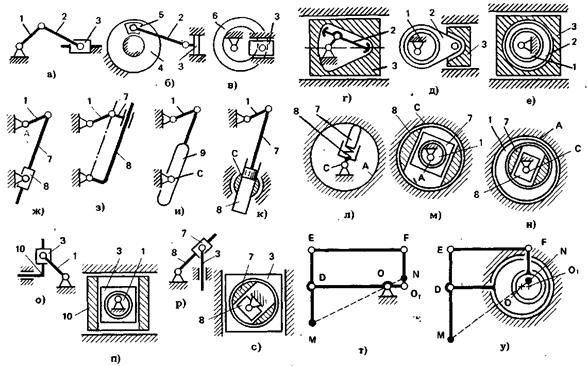
Рис. 2.11

В основу конструктивного преобразования положено совмещение функций звеньев, выполнение элементов шарниров и других кинематических пар большими по размерам, чем размеры звеньев, замена охватывающих элемен­тов охватываемыми, размещение одних звеньев и элементов кинематических пар внутри других элементов ки­нематических пар, замена одних звеньев и кинематических пар другими звеньями и парами с теми же функ­циональными признаками.

На сх. а — структурная схема кривошипно-ползунного механизма: 1 — кривошип; 2 — шатун; 3 — ползун. На сх. б вместо кривошипа выполнен круговой паз. 4, в котором размещен ползун 5. На сх. в кривошип и шатун заменены кулачком б, который взаимодействует с элементом шарнира 3. Таким образом, кривошипно-ползунный механизм преобразован в кулачковый механизм.

На сх. г элементы шарнира, соединяю­щие звенья 2 и 3, выполнены больше шатуна 2, а кривошип 1 и шатун 2 раз­мещены внутри ползуна.

На сх. д кривошип 1 выполнен в виде эксцентрика и помещен внутрь охваты­вающей детали шарнира 1 — 2.

На сх. е кривошип 1 и шатун 2 вы­полнены в виде эксцентриков. Элементы шарниров и звенья размещены внутри ползуна. Такая конструктивная разно­видность имеет большую жесткость в направлении движения ползуна, но более низкий КПД из-за больших углов давле­ния и скоростей скольжения, обуслов­ленных соотношением размеров, по сравнению со схемами, рассмотренными выше.

В сх. ж и з кулиса 8 выполнена соответственно в виде охватывающей и в виде охватываемой деталей, а ползун 7 — наоборот: в виде охватываемой и охватывающей деталей.

В сх. и функции кулисы и ползуна совмещены в звене 9, взаимодействую­щем с элементом шарнира С.

В сх. к ползун и кулиса выполнены в виде поршня 7 и цилиндра 8, разме­щенного внутри шарнира С.

В сх. л функции кривошипа и шар­нира А совмещены в элементе шарнира А, охватывающем все остальные детали. Центр кривизны поверхности А смещен по отношению к центру шарнира С. Ползун 7 с поверхностью А образует высшую кинематическую пару. Кривошипно-кулисный механизм такого типа широко используется в гидромашинах.

В сх. м кривошип 1 выполнен в виде эксцентрика и помещен внутрь ползуна 7, который размещен внутри кулисы 8. Все звенья вместе помещены внутрь шарнира С.

В сх. н выполнено преобразование в обратном порядке по отношению к сх. м. Кулиса 8 размещена в ползуне 7, который находится внутри кривошипа I, выполненного в виде эксцентрика. Все звенья размещены внутри шарнира А.

Принципы, приведенные выше, ис­пользованы при преобразовании сх. о в сх. и и сх. р в сх. с.

В сх. п кривошип 1 в виде эксцент­рика помещен внутрь ползуна 3, который расположен внутри ползуна 10.

В сх. с кулиса 8 помещена внутрь ползуна 7, который находится внутри шарнира 7—3, установленного внутри ползуна 3.

В сх. у шарнир 01 размещен внутри шарнира О. Остальные шарниры О, Е, Р оставлены без изменений по сравнению со сх. т. Воспроизводящая точка М, лежащая на линии МО, размещена на звене ОР также внутри шарнира О. В такой схеме добиваются самоторможения звеньев при внешнем воздействии на звено ОР приложенном в т. N.

Приведенные приемы могут быть ис­пользованы по отношению к другим механизмам. Они позволяют получать механизмы с различ­ными габаритными размерами, силовы­ми и энергетическими характеристи­ками.

Вопросы для самоконтроля:

1. Назовите методы структурного синтеза механизмов.

2. В чем состоит метод наслоения структурных групп?

3. В чем состоит метод инверсии?

4. Как методом наслоения структурных групп получить кривошипно-ползунный или кривошипно-коромысловый механизм?

5. Как инверсией кривошипно-ползунного механизма получить кривошипно-кулисный механизм?

6. Как определить количество избыточных связей в механизме?

7. За счет чего устраняются избыточные связи?

8. В чем заключается метод конструктивного преобразования механизма?