Непрерывное вейвлет-преобразование исходного вейвлета непрерывного

V(x) = (x² - 1) exp(-0,5 x²) – вторая производная Гауссова импульса y(x) = exp(-0,5 x²).

Произведем подстановку 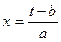Получим функцию базисного вейвлета

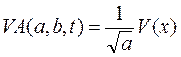
Множитель 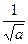необходим для сохранения нормы

||VA(a,b,t)|| = ||v(t)||.

Тогда из (3.1.4.) имеем 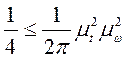, что после преобразования дает (3.1.3.а).

Нетрудно видеть, что равенство в (3.1.4) возможно при φ’(t)=at φ(t).

Отсюда следует, что 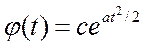. Следовательно, (3.1.3б) справедливо при 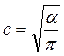и а=-2α.