При некоррелированных погрешностях измерений 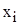 используется метод линеаризации путем разложения функции
используется метод линеаризации путем разложения функции 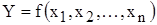 в ряд Тейлора:
в ряд Тейлора:
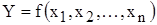
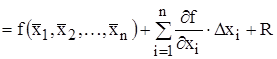 ,
,
где 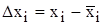 - отклонение отдельного результата наблюдения
- отклонение отдельного результата наблюдения 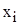 от
от 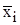 ;
; 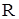 - остаточный член разложения.
- остаточный член разложения.
Остаточным членом пренебрегают, если:
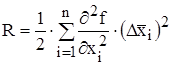 ,
,
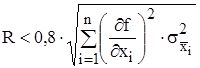 ,
,
где 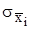 - оценка с.к.о. случайной погрешности результата измерения
- оценка с.к.о. случайной погрешности результата измерения 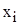 .
.
Результат измерения 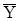 вычисляют по формуле:
вычисляют по формуле:
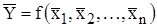 .
.
Оценку с.к.о. случайной составляющей погрешности результата такого косвенного измерения вычисляют по формуле:
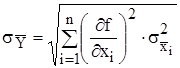 .
.
Доверительные границы:
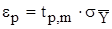 .
.
Абсолютная погрешность косвенного измерения равна:
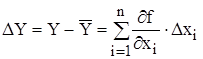 .
.
 2014-01-31
2014-01-31 796
796








