2014-02-01
778
Фактически значения критерия Стьюдента для разностей (q -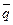 
) и (d – 0) определяются по следующим формулам:
, 
,
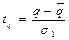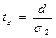где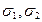 
- среднее квадратическое отклонение для величины S и d;
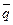- среднее значение величины q для ряда, в котором уровни расположены случайным образом.
Если фактические значения критериев Стьюдента меньше табличных при определенном уровне значимости, то гипотеза об отсутствии тренда в средней и дисперсии подтверждается.
Линейный тренд
Самым простым типом линии тренда является прямая линия, которая описывается линейным уравнением тренда.
Уравнение прямой (линейный тренд):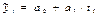 
,
где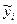 
- выровненные (теоретические) уровни тренда для лет с номером i;
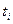- номера моментов или периодов времени, к которым относятся уровни временного ряда (год, месяц, др)
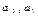- параметры тренда.
Величина параметров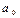 
и 
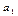определяется по методу наименьших квадратов. Для этого строят систему нормальных уравнений.
