Проверяется гипотеза о существовании разности средних: 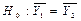 . Для этого временной ряд разбивают на две равные или почти равные части. В качестве критерия проверки гипотезы принимают критерий Стьюдента. Если t
. Для этого временной ряд разбивают на две равные или почти равные части. В качестве критерия проверки гипотезы принимают критерий Стьюдента. Если t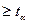 , где t – расчетное значение критерия Стьюдента; t
, где t – расчетное значение критерия Стьюдента; t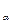 - табличное значение при уровне значимости α, то гипотеза об отсутствии тренда отвергается; если t
- табличное значение при уровне значимости α, то гипотеза об отсутствии тренда отвергается; если t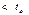 , то гипотеза (H
, то гипотеза (H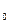 ).
).
| Параметр | Расчет и содержание параметра |
| Число степеней свободы | 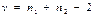
|
| Среднее квадратическое отклонение разности средних | 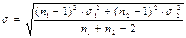 Для расчета дисперсий в каждой части временного ряда выбирается число степеней свободы (
Для расчета дисперсий в каждой части временного ряда выбирается число степеней свободы (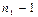 ) и ( ) и (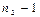 ). Соответственно сама дисперсия i-й части временного ряда определяется по формуле ). Соответственно сама дисперсия i-й части временного ряда определяется по формуле
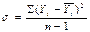 , i = 1, 2, …, n.
Гипотезу о равенстве дисперсий проверяют с помощью критерия Фишера:
F = , i = 1, 2, …, n.
Гипотезу о равенстве дисперсий проверяют с помощью критерия Фишера:
F =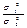 , где , где 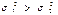 .
Если фактическое значение критерия Фишера меньше табличного значения при заданном уровне вероятности, то гипотеза о равенстве дисперсий принимается.
Если фактическое значение критерия Фишера больше табличного, то гипотеза о равенстве дисперсий отвергается; тогда критерий Стьюдента для проверки существенности разности средних не может быть использован. .
Если фактическое значение критерия Фишера меньше табличного значения при заданном уровне вероятности, то гипотеза о равенстве дисперсий принимается.
Если фактическое значение критерия Фишера больше табличного, то гипотеза о равенстве дисперсий отвергается; тогда критерий Стьюдента для проверки существенности разности средних не может быть использован.
|
Расчетное значение критерия Стьюдента определяется по следующей формуле:
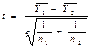 ,
,
где 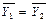 - средние для каждой части временного ряда;
- средние для каждой части временного ряда; 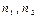 - число наблюдений в каждой из частей ряда; σ - среднее квадратическое отклонение разности средних.
- число наблюдений в каждой из частей ряда; σ - среднее квадратическое отклонение разности средних.
2. Метод Фостера – Стюарта определяется наличие тенденции явления и тренд дисперсии уровней временного ряда. Часто этот метод используют при детальном анализе временного ряда и построении по нему прогнозов.
При использовании этого метода вычисления строят в определенной последовательности.
Этапы вычисления наличия тренда при использовании метода Фостера – Стюарта:
1. Сравнение каждого уровня временного ряда со всеми предыдущими уровнями. Сравнение проводят по следующим неравенствам: если Y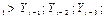 …; Y
…; Y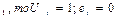 ;
;
если Y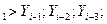 …; Y
…; Y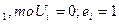 ;
;
2. Вычисление значений величин q и d. Вычисления строят по следующим формулам: q = 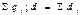 ,
,
где 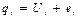 ;
; 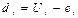 .
.
Величина q характеризует тенденцию изменения дисперсии временного ряда и принимает значения в пределах 0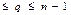 . Если все уровни ряда равны между собой, то q =0. Если уровни временного ряда монотонно убывают или возрастают, q = n-1. Величина d характеризует тенденцию изменения средней и имеет два предела – нижний и верхний. Нижний предел d = - (n – 1) характеризует монотонно убывающий ряд; верхний предел d = (n-1) характеризует монотонно возрастающий ряд. Величина d может быть равна 0, но такие случаи в практических расчетах крайне редки.
. Если все уровни ряда равны между собой, то q =0. Если уровни временного ряда монотонно убывают или возрастают, q = n-1. Величина d характеризует тенденцию изменения средней и имеет два предела – нижний и верхний. Нижний предел d = - (n – 1) характеризует монотонно убывающий ряд; верхний предел d = (n-1) характеризует монотонно возрастающий ряд. Величина d может быть равна 0, но такие случаи в практических расчетах крайне редки.
 2014-02-01
2014-02-01 749
749








