| Параметр уравнения | Содержание параметров |
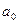
| Коэффициент тренда, численно равный среднему выровненному уровню для момента или периода времени, принятого за начало отсчета (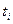 = 0) = 0)
|
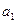
| Коэффициент тренда, характеризующий средний за весь период среднегодовой прирост, который уже не является константой, а изменяется равномерно со среднем ускорением, равным 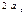
|
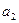
| Главный параметр уравнения, константа, характеризующая ускорение |
Основные свойства параболического тренда:
- Наблюдаются неравные, но равномерно возрастающие или равномерно убывающие абсолютные изменения за равные промежутки времени.
- Парабола имеет две ветви: восходящую с увеличением уровней признака и нисходящую с их уменьшением.
- Поскольку свободный член уравнения 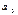 как значение показателя в начальный момент отсчета времени обычно бывает величиной положительной, характер тренда определяется знаками параметров
как значение показателя в начальный момент отсчета времени обычно бывает величиной положительной, характер тренда определяется знаками параметров 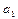 и
и 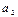 :
:
а) при 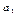 > 0 и
> 0 и 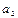 > 0 имеет место восходящая ветвь, т.е. тенденция к ускоренному росту уровней;
> 0 имеет место восходящая ветвь, т.е. тенденция к ускоренному росту уровней;
б) при 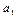 < 0 и
< 0 и 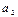 < 0 имеет место нисходящая ветвь, т.е. тенденция к ускоренному сокращению уровней;
< 0 имеет место нисходящая ветвь, т.е. тенденция к ускоренному сокращению уровней;
в) 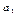 > 0 и
> 0 и 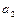 < 0 имеет место либо восходящая ветвь с замедляющимся ростом уровней, либо обе ветви параболы – восходящая и нисходящая, если их считать единым процессом;
< 0 имеет место либо восходящая ветвь с замедляющимся ростом уровней, либо обе ветви параболы – восходящая и нисходящая, если их считать единым процессом;
г) при 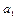 < 0 и
< 0 и 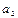 > 0 имеет место либо нисходящая ветвь с замедляющимся сокращением уровней, либо обе ветви – нисходящая и восходящая, если их считать единой тенденцией.
> 0 имеет место либо нисходящая ветвь с замедляющимся сокращением уровней, либо обе ветви – нисходящая и восходящая, если их считать единой тенденцией.
- Цепные темпы изменений либо уменьшаются, либо некоторое время возрастают, но при достаточно длительном периоде рано или поздно темпы роста обязательно начинают уменьшаться, а темпы сокращения уровней при 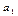 < 0 и
< 0 и 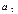 < 0 обязательно начинают возрастать (по абсолютной величине относительного изменения).
< 0 обязательно начинают возрастать (по абсолютной величине относительного изменения).
Для вычисления параметров 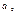 ,
, 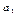 ,
, 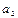 по методу наименьших квадратов строят следующую систему нормальных уравнений с тремя неизвестными.
по методу наименьших квадратов строят следующую систему нормальных уравнений с тремя неизвестными.
Система нормальных уравнений для параболического тренда:
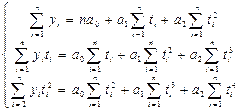
При переносе начала отсчета периодов (моментов) времени в середину ряда, суммы нечетных степеней номеров этих периодов 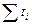 и
и 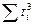 равняются нулю. Следовательно, второе уравнение становится уравнением с одним неизвестным. Отсюда можно выразить параметр
равняются нулю. Следовательно, второе уравнение становится уравнением с одним неизвестным. Отсюда можно выразить параметр 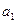 :
: 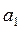 =
= 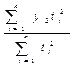
Оставшиеся уравнения образуют систему двух уравнений с двумя неизвестными:
Сокращённая система уравнений для параболического тренда:
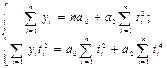
Параболическое уравнение тренда достаточно редко встречается в анализе экономических явлений и процессов.
Гиперболический тренд
Одна из простых форм гиперболы – уравнение, имеющие следующий вид: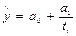
При расчете гиперболического тренда нельзя нумеровать периоды времени от середины ряда, так как значения 1/ 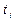 должны быть всегда положительными.
должны быть всегда положительными.
Основные свойства гиперболического тренда:
- При 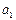 > 0 – уровни медленно снижаются и y
> 0 – уровни медленно снижаются и y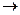
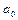 ; также уменьшаются отрицательные абсолютные изменения и величины положительного ускорения; цепные темпы изменения растут и стремятся к 100%.
; также уменьшаются отрицательные абсолютные изменения и величины положительного ускорения; цепные темпы изменения растут и стремятся к 100%.
- При 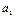 < 0 – уровни замедлено возрастают и
< 0 – уровни замедлено возрастают и 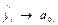 ;также уменьшаются положительные абсолютные изменения и величины отрицательного ускорения; цепные темпы роста замедленно уменьшаются, стремясь к 100%.
;также уменьшаются положительные абсолютные изменения и величины отрицательного ускорения; цепные темпы роста замедленно уменьшаются, стремясь к 100%.
 2014-02-01
2014-02-01 823
823








