График 6.2
График 6.1
Динамика повозрастной смертности в России в 90-е гг. (логарифмическая шкала)
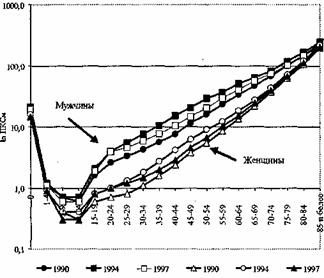
Специалисты считают повозрастные коэффициенты смертности наилучшим инструментом анализа этого демографического процесса. Недостатком является, пожалуй, их большое (до сотни) количество, а также некоторая подверженность влиянию возрастной аккумуляции. Но эти недостатки устраняются расчетом коэффициентов не для одногодичных, а для пятилетних возрастных интервалов. Пятилетние коэффициенты свободны от недостатков одногодичных, а их точность вполне достаточна для большинства практических целей. На графике 6.1 показана динамика повозрастных коэффициентов смертности в России за 90-е гг. На графике 6.2 приведены данные, иллюстрирующие соотношение мужской и женской смертности в нашей стране в те же годы.
Среди повозрастных коэффициентов смертности особое место занимает коэффициент младенческой смертности, т.е. показатель, измеряющий смертность детей в возрасте до года.
|
|
|
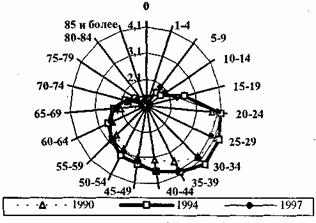
Смертность в возрасте до года, с одной стороны, резко превышает смертность в других возрастах, кроме самых старших. С другой же стороны, величина младенческой смертности служит мощным и весьма информативным показателем уровня социально-экономического развития страны.
Коэффициент младенческой смертности рассчитывается не так, как остальные повозрастные коэффициенты. По своей природе показатель младенческой смертности является, строго говоря, не коэффициентом, а вероятностью. При его вычислении число смертей детей в возрасте до 1 года делится не на их среднегодовую численность, а на число родившихся. Дело в том, что для этой возрастной группы понятие среднегодовой численности практически неопределимо. К тому же вероятности смерти в начале и в конце первого года жизни сильно отличаются друг от друга.
Если мы посмотрим на совокупность умерших в течение календарного года в возрасте 0 лет, то увидим, что эта совокупность образуется из детей, родившихся как в данном, так и в прошлом году (график 6.3). В квадрате ABCD расположены смертные точки детей, умерших в 2000 г. в возрасте до 1 года. Прекрасно видно, что часть этих детей (элементарная совокупность, изображаемая треугольником ACD) родилась в том же 2000 г., а другая (элементарная совокупность, изображаемая треугольником ABC) - в 1999 г.
Расчетная формула для вероятности (коэффициента) смертности на первом году жизни должна, очевидно, учитывать факт принадлежности умерших к разным поколениям. Это делается с помощью различных приближений, выбор которых определяется наличием соответствующей статистической информации и требуемой точностью вычислений.
|
|
|
Если известны только общие данные о числах родившихся и умерших в том или ином году и не нужна большая точность оценки величины коэффициента младенческой смертности, то оценка коэффициента младенческой смертности может быть получена с помощью простого деления числа умерших детей на число родившихся в том же году. Однако эта оценка будет наиболее грубой и приблизительной. К тому же делать это можно только тогда, когда годовые колебания как чисел родившихся, так и чисел умерших невелики. Если же соседние годы сильно отличаются друг от друга в этом отношении, то величина ошибки оценки может выйти за допустимые пределы. В этом случае прибегают к т.н. формуле Ратса, названной так по имени предложившего ее немецкого статистика и демографа Йоханнеса Ратса (1854-1933). В своем общем виде формула Ратса выглядит следующим образом:
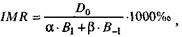
где IMR - коэффициент младенческой смертности: D0 - число детей в возрасте до 1 года, умерших в данном году; В_1 - число родившихся в прошлом году; В1 - число родившихся в данном году: (a и b - веса, причем и b = 1.
Веса и b подбираются, исходя из распределения умерших детей по месяцам первого года жизни. Если бы это распределение было равномерным, т.е. если бы вероятность умереть была одинаковой для любого месяца 1 года жизни, то = 1/2. В действительности же это не так: вероятность смерти уменьшается с возрастом. Чем старше ребенок, тем меньше вероятность того, что он умрет, не дожив до года. При этом одновременно с уменьшением младенческой смертности происходит ее сдвиг к самым ранним возрастам. Поэтому с течением времени весовые коэффициенты в формуле Ратса приходится менять. Ратс принимал a = 2/3, b = 1/3. В настоящее время эти веса чаще всего принимаются равными соответственно 3/4 и 1/4. В некоторых странах, где уровни младенческой смертности малы, в качестве весов принимаются значения a = 4/5 и b = 1/5 или даже более резко отличающиеся друг от друга.
 2013-12-31
2013-12-31 714
714








