3.1 Расчет показателей надежности буровой лебедки
Наработка до отказа буровой лебедки ЛБУ-1200 в часах по данным Уфимского УБР:
166, 147, 151, 133, 151, 176, 170, 172, 184, 141, 138, 175, 202, 173, 149, 142, 130, 149,149, 144, 171, 153, 176, 131, 157, 133, 154, 178, 133, 194, 188, 138, 139, 166, 145, 160, 132, 157, 172, 143, 184, 157, 141, 124, 156, 140, 201, 156, 232, 149, 139, 154, 214, 154, 173, 188, 133, 177, 144, 221, 138, 157, 134, 163, 144, 158, 143, 179, 122, 174, 151, 159, 140, 182, 216, 207, 212, 199, 202, 181.
n=80
Найдем число интервалов:
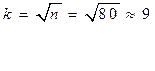
Определим величину одного интервала:
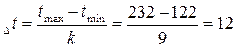
где tmax, tmin – соответственно наибольшее и наименьшее значения случайной величины.
При составлении статистического ряда для каждого интервала подсчитывают:
ni – количество значений случайной величины в i-ом интервале;
pi=ni/n – частность (опытная вероятность) в i-ом интервале;
f(t)=pi/Dt – эмпирическую плотность вероятности;
F(t)=S(ni/n) – эмпирическую вероятность отказов.
Таким образом, строим статистический ряд представленный в таблице 8.1.
Таблица 3.1 – Статистический ряд
| Интервал, ч | Середина интервала, ti, ч | Частота ni | Опытная вероятность pi=ni/n | F(t)=S(ni/n) | f(t)=pi/Dt |
| 100-124 124-136 136-148 148-160 160-172 172-184 184-196 196-208 208-220 220-232 | 0,025 0,1 0,2125 0,25 0,0875 0,1625 0,0375 0,0625 0,0375 0,025 | 0,025 0,125 0,3375 0,5875 0,675 0,8375 0,875 0,9375 0,975 | 0,0021 0,0083 0,0177 0,0208 0,0073 0,0135 0,0031 0,0052 0,0031 0,0021 |
Определим среднее значение для статистического ряда:
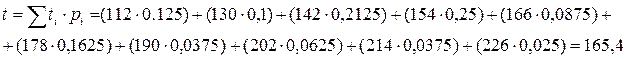
Определим среднее квадратичное отклонение:
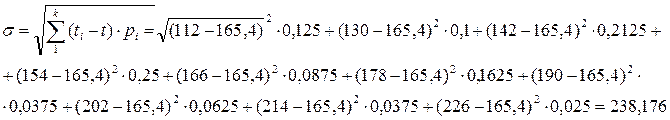
Определим коэффициент вариации:
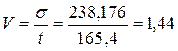
Зная коэффициент вариации можно определить параметр распределения Вейбулла – b и коэффициент [Кb] b=0,7; Kb=1,266.
Параметр а подсчитываем по выражению: 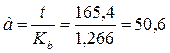
Рекомендуется в первом приближении принимать распределение Вейбулла при V>0,5. Так как в нашем случае V=1,44 значит, принимаем распределение Вейбулла.
Строим теоретические кривые функции плотности распределения наработки f(t), теоретическую вероятность безотказной работы P(t), теоретическую функцию распределения отказности F(t) и функцию интенсивности отказов l(t). Для этого найдем эти значения.
Вычислим значения функции плотности распределения наработки f(t),
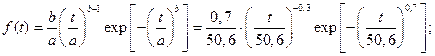
Таблица 3.2 – Функция плотности распределения f(t)
| t | |||||||||||
| f(t) | 0.0095 | 0.0070 | 0.0053 | 0.0042 | 0.0034 | 0.0028 | 0.0024 | 0.0020 | 0.0017 | 0.0014 |
Вычислим значения теоретической вероятности безотказной работы P(t) на каждом интервале по формуле:
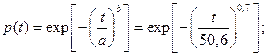
Таблица 3.3 – Вероятность безотказной работы P(t)
| t | |||||||||||
| P(t) | 0,552 | 0,455 | 0,381 | 0,324 | 0,278 | 0,240 | 0,208 | 0,182 | 0,160 | 0,141 |
Вычислим значения теоретической функции распределения отказности F(t) по формуле:
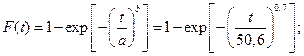
Таблица 3.4 – Функция распределения отказности F(t)
| t | |||||||||||
| F(t) | 0,448 | 0,545 | 0,619 | 0,676 | 0,722 | 0,760 | 0,792 | 0,818 | 0,840 | 0,859 |
Вычислим значения функции интенсивности отказов по формуле:
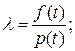
Таблица 3.5 – Функция интенсивности отказов l(t)
| t | |||||||||||
| l(t) | 0,0172 | 0,0153 | 0,0139 | 0,0129 | 0,0122 | 0,0116 | 0,0115 | 0,0111 | 0,0106 | 0,0099 |
Проверим гипотезу по критериям согласия о правильности выбранного закона
Критерий Пирсона: 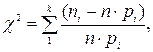
где k – число интервалов статистического ряда;
ni – частота в i-ом интервале;
n – общее число значений случайной величины;
pi – теоретическая вероятность попадания случайной величины в i-ом интервале
pi=piн-pik,
где piн и pik – функция вероятности в конце и в начале i-го интервала.
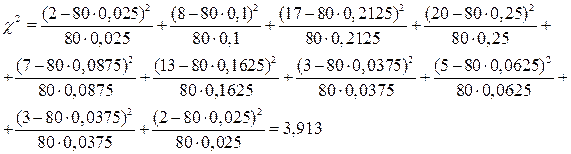
Число степеней свободы r=k – s=10 – 3=7. При r=7 и c2=3,913 вероятность совпадения теоретического и статического распределения Р=0,7≥0,1, что подтверждает принятую нами гипотезу о распределении наработки до отказа по закону Вейбулла.
Критерий Колмогорова. Значение вероятности попадания случайной величины приведено в таблице 3.6.
Таблица 3.6 – Значение вероятности попадания случайной величины
| t, z | P(t)теор | Pi | F(t)теор | F(t)опытн | ½D½=F(t)т-F(t)o |
| 0,552 0,455 0,381 0,324 0,278 0,240 0,208 0,182 0,160 0,141 | 0,448 0,097 0,074 0,057 0,046 0,038 0,032 0,026 0,022 0,019 | 0,448 0,545 0,619 0,676 0,722 0,760 0,792 0,818 0,840 0,859 | 0,025 0,125 0,3375 0,5875 0,675 0,8375 0,875 0,9375 0,975 | 0,423 0,42 0,2815 0,0885 0,047 0,0775 0,083 0,1195 0,135 0,141 |
 2013-12-31
2013-12-31 820
820








