Будущая стоимость аннуитета

Будущая стоимость единицы (накопленная сумма единицы).

Сложного процента

Характеристика шести стандартных функций

Функция

Общая характеристика. Назначение

1. Будущая стоимость единицы (FV)

Значение функции отражает процесс наращения (увеличения) первоначальной суммы денег, положенной на депозит при накоплении по сложному проценту, в связи с присоединением процентов к первоначальной сумме. Она позволяет решать задачи типа: «Определить сумму денежных средств, которая будет выдана вкладчику банком, если на первоначальный взнос PV в течении n лет m раз в год будет начисляться годовая процентная ставка».

Окончание табл. 4

Функция	Общая характеристика. Назначение
2. Будущая стоимость аннуитета (FVA)	Позволяет решать задачу типа: «Определить размер денежных средств на счете вкладчика. Если течении n лет m раз в год вносить фиксированную сумму денежных средств PMT при начислении банком процентов на данный вклад.
3. Дисконтирование. (Текущая стоимость единицы) (PV)	Функции позволяет решать задачи типа: «Определить размер денежных средств PV, который необходимо внести на депозит сегодня, чтобы через n лет при начислении m раз в год и определенной процентной ставке накопить определенную сумму денежных средств».
4. Текущая стоимость аннуитета (PVA)	Позволяет решить задачи типа: «Определить размер денежных средств, которые необходимо поместить на депозит сегодня при годовой процентной ставке, чтобы в течении n лет m раз в год снимать со счета определенные равные суммы денежных средств PMT».
5. Периодический взнос в погашение кредита (А)	Позволяет решать задачи типа «Определить равновеликий размер денежных средств, который можно снимать со счета n раз в год, если известен первоначальный капитал и процентная годовая ставка».
6. Периодический взнос на накопление фонда (А ф)	Позволяет решать задачи типа: «Определить размер денежных средств, который необходимо с периодичностью m раз в год вносить в течении n лет на пополняемый депозит, чтобы накопить определенный капитал.

Рассмотрим применение данных формул при оценке денежных потоков объектов недвижимости.

Эта функция позволяет определить стоимость объекта недвижимости или финансовых потоков, связанных с использованием объекта недвижимости в будущем времени:

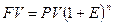,(4)

где FV – будущая стоимость объекта недвижимости, руб.; PV – текущая стоимость объекта недвижимости, руб.

В случае применения эффективной ставки процента (нормы доходности) эта формула примет вид:

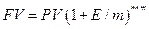, (5)

Пример 1:

Объект недвижимости был приобретен за 10 млн руб. Какова будет стоимость объекта через два года, если ежегодный рост стоимости на данном сегменте рынка недвижимости составляет 5 %?

Решение:

Дано: PV = 1; Е = 0,05; n = 3

FV = 10 (1 + 0,05)² = 11,025 млн руб.

Пример 2:

Какова будет предположительно стоимость жилья через два года, если на текущий момент времени средняя стоимость одного квадратного метра жилья составляла 30 тыс. руб., а ежеквартальный рост цен на жилую недвижимость прогнозируется на уровне 1 %.

Решение:

Дано: PV = 30; е = 0,01; n = 2; m = 4.

FV = 30 (1 + 0,01)^{2 × 4} = 32,5 тыс. руб. за м².

Эта функция позволяет определить будущую стоимость аннуитетных поступлений:

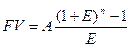. (6)

В случае осуществления более частых поступлений:

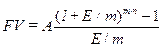. (7)

Пример 3:

Определить размер денежных средств, накопленных на счете в течение 3 лет для покупки объекта недвижимости, если ежегодно вносить 280 тыс. руб. на депозит под 9 % годовых.

Решение:

Дано: A = 280; Е = 0,09; n = 3.

FVA = 280{[(1 + 0,09)³ – 1] / 0,09} = 918 тыс. руб.

Пример 4:

Семья предполагает приобрести через 3 года квартиру. С этой целью открыт жилищный накопительный счет в банке, на который в конце каждого квартала вносятся по 70 тыс. руб. Какая сумма накопится на счете через три года, если по счету начисляется 9% годовых?

Решение:

Дано: A = 70, Е = 0,09, n = 3, m = 4.

FVA = 70{[(1 + 0,09 / 4)^3×4 – 1] / (0,09 / 4)} = 952,16 тыс. руб.

В данном примере можно увидеть преимущество применения эффективной ставки доходности: чем чаще осуществляются взносы на счет, тем больше накопленная сумма.