2014-01-24
717
Большое количество прикладных задач в технике, и в электротехнике в частности, решаются с использованием систем линейных уравнений. Поэтому весьма важно владеть методикой их решения. Существует достаточное количество как ручных способов их решения, так и способов решения с помощью компьютера. Имеется ряд прикладных программ таких как Matlab, Matcad и других, позволяющих достаточно просто решать такую задачу. Но вместе с тем и программа MS Excel предлагает свои возможности для решения систем n линейных уравнений с n неизвестными.
Запись вида
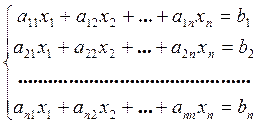
где аij – произвольные числа, являющиеся коэффициентами при неизвестных,
xi – неизвестные, подлежащие вычислению,
bi – произвольные числа, представляющие собой свободные члены.
Такая форма записи системы линейных уравнений называется нормальной формой.
Если система уравнений имеет хотя бы одно решение, то она называется совместной, в противном случае – она несовместна.
Если система уравнений имеет только одно решение, то она называется определенной, если она имеет несколько решений, то ее называют неопределенной.
Приведенную систему уравнений можно представлять и в матричном виде:
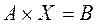
где А – матрица коэффициентов или матрица системы:
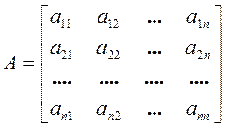
X – матрица – столбец (вектор) неизвестных
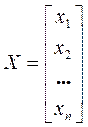
В – матрица – столбец (вектор) свободных членов
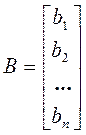
В развернутом виде систему можно записать следующим образом:
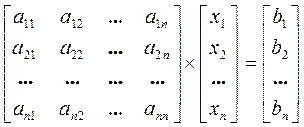
Существует ряд методов решения таких систем, в частности, метод Крамера, Гаусса, обратной матрицы и др. Наиболее удобным методом решения такого вида систем уравнений с помощью программы MS Excel является метод обратной матрицы. Решение системы с помощью этого способа представляется в виде:
.
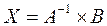Программа MS Excel располагает необходимыми средствами для нахождения обратной матрицы и умножения матриц, что обеспечивает решения системы уравнений.
Порядок операций для решения системы линейных уравнений средствами MS Excel следующий:
– ввести (разместить) матрицу коэффициентов А в определенной области электронной таблицы,
– ввести матрицу – столбец свободных членов В,
– выделить область ячеек под обратную матрицу (такого же размера, как и под матрицу коэффициентов А),
– щелкнуть по кнопке Вставки функции,
– в раскрывшемся окне Мастер функций, в поле Категория, выбрать строку Математические, а в поле Функция – имя функции МОБР,
– щелкнуть по кнопке ОК,
– в раскрывшемся окне МОБР, в рабочем поле Массив, указать диапазон ячеек, занимаемый исходной матрицей А,
– нажать сочетание клавиш Ctrl+Shift+Enter.
Если обратная матрица не появилась в указанном диапазоне, то следует щелкнуть мышью в строке формул и повторить нажатие клавиш Ctrl+Shift+Enter.
– выделить диапазон ячеек под матрицу – столбец (из n ячеек) неизвестных Х,
– щелкнуть по кнопке Вставки функции,
– в раскрывшемся окне Мастер функций, в поле Категория, выбрать строку Математические, а в поле Функция – имя функции МУМНОЖ,
– щелкнуть по кнопке ОК,
– в раскрывшемся окне МУМНОЖ, в рабочем поле Массив1 ввести диапазон ячеек, занимаемой обратной матрицей А-1, а в рабочем поле Массив2 ввести диапазон ячеек, занимаемой обратной матрицей – столбцом свободных членов В,
– нажать сочетание клавиш Ctrl+Shift+Enter.
Если вектор Х не появится в указанном диапазоне, то следует щелкнуть мышью в строке формул и повторить нажатие клавиш Ctrl+Shift+Enter.
После получения решения следует произвести проверку результата, выполнив операцию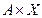 
. Полученный результат должен быть равен вектору В.
