2014-01-24
717
Лекция 7.2. Схемы алгоритма
Логическая структура алгоритма решения любой задачи может быть выражена комбинацией трех базовых структур: следования, ветвления и цикла (это содержание теоремы Бема – Якопини).
Линейная структура (следование) самая важная из структур. Она означает, что действия могут быть выполнены друг за другом (рис. 5.2.1.).
|
|
 |  |  |
Прямоугольники могут представлять как одну единственную команду, так и множество операторов, необходимых для выполнения сложной обработки данных.
Пример 7.2.1.
Опишем алгоритм сложения двух чисел на псевдокоде и в виде блок-схемы (рис. 7.2.2.).
1. Псевдокод:
2. Ввод двух чисел a, b
3. Вычисляем сумму S = a + b
4. Вывод S
5. Конец.
Рис. 7.2.2. Блок - схема к примеру 7.2.1.
Ветвление (развилка) – это структура, обеспечивающая выбор между двумя альтернативами. Выполняется проверка условия, а затем выбирается один из путей (рис. 5.2.3).
Вход
 |
Ложь (НЕТ) Истина (ДА)
 |
Выход
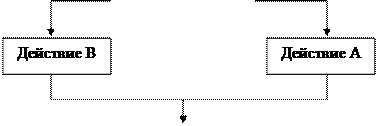
Рис. 7.2.3. Полное ветвление
Если условие имеет значение «Истина», то выполняется «Действие А». Если условие имеет значение «Ложь», выполняется «Действие В». Эта структура называется, также «Если – ТО – ИНАЧЕ» или «развилка». Каждый путь (ТО или ИНАЧЕ) ведет к общей точке слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран. Может оказаться, что для одного из результатов проверки ничего выполнять не надо. В этом случае можно применить только один обрабатывающий блок (рис. 5.2.4).
 |
Вход
ДА НЕТ
 |
Выход
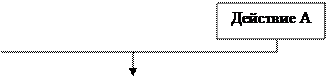
Рис. 7.2.4. Структура «неполное ветвление»
Такая структура называется «неполным ветвлением» или «неполной развилкой».
Пример 7.2.2.
Вывести значение наибольшего числа из двух чисел (рис. 5.2.5).
Псевдокод:
1. Ввод двух чисел a, b
2. 
ЕСЛИ a>b, ТО «выводим a»,
ИНАЧЕ «выводим b»
3. 
|
|
Конец.
НЕТ ДА
Рис. 7.2.5. Блок – схема к примеру 5.2.2.
Цикл (или повторение) предусматривает повторное выполнение некоторого набора команд алгоритма. Циклы позволяют записать длинные последовательности операций обработки данных с помощью небольшого числа повторяющихся команд. Различают два типа циклов: «цикл с предусловием» и «цикл с постусловием».
Цикл с предусловием («Пока») (рис. 5.2.6).
|
 | |||||
 |  | ||||
Ложь
Рис. 7.2.6. Структура цикла «Пока».
Цикл начинается с проверки логического выражения. Если оно истинно, то выполняется тело цикла, затем все повторяется, пока логическое выражение сохраняет значение «истина». Как только оно становится ложным, выполнение операций прекращается и управление передается дальше. Особенностью цикла с предусловием является то, что если изначально логическое выражение имеет значение «ложь», то тело цикла не выполнится ни разу.
