Возьмем функцию 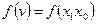 двух переменных x1x0. Применим к ней терему разложения для переменной x1.
двух переменных x1x0. Применим к ней терему разложения для переменной x1.
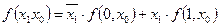
Далее каждую из функций 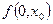 и
и 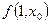 разложим по переменной x0.
разложим по переменной x0.
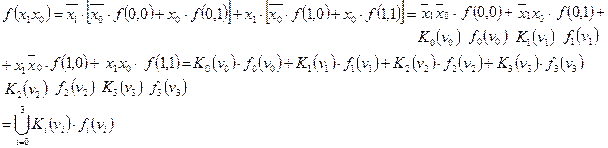
Такая форма представления функции называется совершенной дизъюнктивной нормальной формой (СДНФ).
В общем виде представление функции в СДНФ:
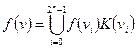 Так как значение функции
Так как значение функции 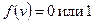 то
то 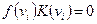 если
если 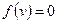 и
и 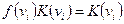 если
если 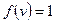 отсюда СДНФ можно представить в виде:
отсюда СДНФ можно представить в виде:
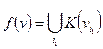 где i1 – номера точек, в которых функция
где i1 – номера точек, в которых функция 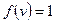 .
.
СДНФ можно получить аналогичным способом с помощью теоремы разложения. Но можно пойти более легким путем.
Возьмем инверсию СДНФ: 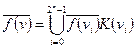 из данного соотношения на основании закона двойственности получим:
из данного соотношения на основании закона двойственности получим: 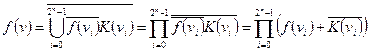 а так как
а так как 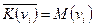 общий вид СКНФ:
общий вид СКНФ:
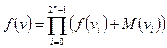
Так как значение функции 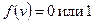 то
то 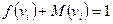 если
если 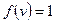 и
и 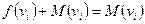 если
если 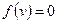 отсюда СКНФ можно представить в виде:
отсюда СКНФ можно представить в виде:
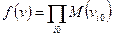 где i0 – номера точек, в которых функция
где i0 – номера точек, в которых функция 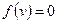 .
.
 2014-01-24
2014-01-24 945
945








