Минимизация логических функций

Одной из основных задач, возникающих при синтезе комбинационных схем (КС), является минимизация логических функций, которые эти КС реализуют. Чем проще логическое выражение, описывающее функцию, тем проще и дешевле реализующая ее КС.

В качестве критерия сложности логического выражения, описывающего функцию, целесообразно принять числи первичных термов 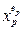, в него входящих.

Существуют два метода минимизации:

аналитический, весьма трудоемок и требует не тривиального подхода, который не всегда виден;

графический, наиболее нагляден, прост в использовании, но может иметь некоторые ограничения.

Очевидно, что любой метод минимизации может основываться только на тождественном преобразовании логических выражений.

4.11.1. Конъюнктивные и дизъюнктивные термы

Конъюнктивным термом (контермом) называется: конъюнкция любого числа первичных термов, если каждый первичный терм с индексом p входит в него не более одного раза.

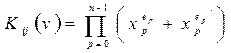- функция 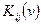представляет собой конъюнкцию первичных термов.

Дизъюнктивным термом (дизтермом) называется: дизъюнкция любого числа первичных термов, если каждый первичный терм с индексом p входит в нее не более одного раза.

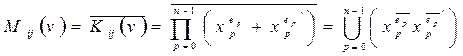- функция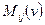представляет собой дизъюнкцию первичных термов.

Пример: Возьмем две точки области определения функции трех переменных i=1₁₀ (001)₂и j=5₁₀ (101)₂. Выразим эти точки через термы .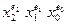

Для точки i -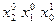

Для точки j -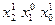

1. Сложим первичные термы с одинаковыми индексами точки i и точки j соответственно.

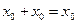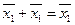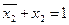, , - перемножим полученные результаты 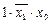получим: 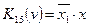- контерм точек 1 и 5 области определения функции трех переменных.

2. Перемножим первичные термы с одинаковыми индексами точки i и точки j соответственно, при этом проведем инверсию каждого терма, 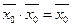, , 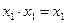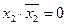сложим полученные результаты, 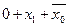получим: 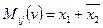- дизтерм точек 1 и 5 области определения функции трех переменных.