Совокупность элементарных функций, с помощью которых можно записать любую функцию 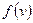 , называется функционально полной системой функций или базисом. Из выше приведенного параграфа можно сделать вывод, что для представления любой функции
, называется функционально полной системой функций или базисом. Из выше приведенного параграфа можно сделать вывод, что для представления любой функции 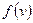 , в СДНФ и СКНФ достаточно использовать только функции (операции) И, ИЛИ и НЕ, т.е. совокупность этих функций является базисом.
, в СДНФ и СКНФ достаточно использовать только функции (операции) И, ИЛИ и НЕ, т.е. совокупность этих функций является базисом.
Преобразуем СДНФ функции с помощью законов двойного отрицания и де Моргана:
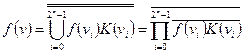 Данная форма представления функции называется совершенной нормальной формой (СНФ) в базисе И-НЕ, так как она требует использования только функций (операций) И-НЕ.
Данная форма представления функции называется совершенной нормальной формой (СНФ) в базисе И-НЕ, так как она требует использования только функций (операций) И-НЕ.
Проведем аналогичные действия с СКНФ:
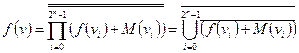
Данная форма представления функций называется СНФ в базисе ИЛИ-НЕ, так как она требует использования только функций (операций) ИЛИ-НЕ.
 2014-01-24
2014-01-24 765
765








