Общие правила можно установить только для случаев, когда в результате минимизации получаются так называемые минимальные нормальные формы (МНФ) функций.
Есть понятие соседних минтермов (макстермов): - два минтерма 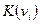 и
и 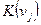 будем называть соседними, если они различаются только одним первичным термом
будем называть соседними, если они различаются только одним первичным термом 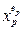 , т.е. для одного из минтермов ep=0, а для другого ep=1 (все же остальные первичные термы одинаковые)
, т.е. для одного из минтермов ep=0, а для другого ep=1 (все же остальные первичные термы одинаковые)
Например: если n=3, то минтермы 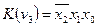 и
и 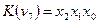 являются соседними, так как они различаются только одним первичным термом
являются соседними, так как они различаются только одним первичным термом 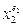 . Для минтерма
. Для минтерма 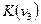 соседними являются также минтермы
соседними являются также минтермы 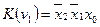 и
и 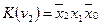 . Отсюда можно сказать, что каждый минтерм n переменных
. Отсюда можно сказать, что каждый минтерм n переменных 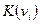 имеет по n соседних минтермов из общего числа 2n минтермов.
имеет по n соседних минтермов из общего числа 2n минтермов.
Рассмотрим контерм n переменных 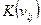 , не зависящий от одной переменной, т.е. случай, когда контерм является конъюнкцией (n-1)-го первичного терма. Данный контерм можно представить в виде
, не зависящий от одной переменной, т.е. случай, когда контерм является конъюнкцией (n-1)-го первичного терма. Данный контерм можно представить в виде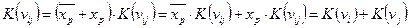 . Очевидно, что полученные минтермы
. Очевидно, что полученные минтермы 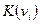 и
и 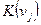 являются соседними, так как они различаются только одним первичным термом
являются соседними, так как они различаются только одним первичным термом 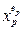 . Отсюда следует правило минимизации: дизъюнкцию двух соседних минтермов можно заменить одним контермом, независящим от одной переменной.
. Отсюда следует правило минимизации: дизъюнкцию двух соседних минтермов можно заменить одним контермом, независящим от одной переменной.
Если минтерм имеет два соседних минтерма, то их можно заменить двумя контермами независящих от соответствующих переменных, так как согласно закону 1.6 (x+x=x) минтерм, который соседний с двумя другими, можно заменить на дизъюнкцию любого числа равных ему минтермов. В результате такого объединения можно получить контермы соседние друг с другом. Их так же можно объединить, получая из двух соседних контермов, независящих от одной переменной, один контерм, независящий од двух переменных. Такая процедура проводится до тех пор пока функция будет состоять только из не соседних контермов или минтермов.
Исходя из выше сказанного, можно установить общее правило минимизации: одним контермом n переменных 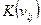 , не зависящим от m переменных
, не зависящим от m переменных 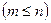 , можно заменить дизъюнкцию 2m минтермов, если каждый из них имеет по m соседних минтермов среди остальных 2m-1 минтермов.
, можно заменить дизъюнкцию 2m минтермов, если каждый из них имеет по m соседних минтермов среди остальных 2m-1 минтермов.
В результате таких операций получается функция: 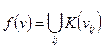 - такая форма представления функции называется ДНФ, а если она содержит минимально возможное число первичных термов
- такая форма представления функции называется ДНФ, а если она содержит минимально возможное число первичных термов 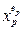 , то она называется минимальной ДНФ (МДНФ).
, то она называется минимальной ДНФ (МДНФ).
Получение минимальной конъюнктивной нормальной формы (МКНФ) сводится к нахождению двойственной функции от МДНФ, в результате чего получаем: 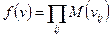
 2014-01-24
2014-01-24 1088
1088
