Разработка выборочного плана и объема выборки

Данный этап реализуется в такой последовательности:

1. Выделение объектов генеральной совокупности. Генеральная совокупность – это множество всех единиц, являющихся объектами исследования. Генеральной совокупностью могут быть рынок в целом, сегмент рынка и целевая группа сегментов.

2. Определение методов обследования. В зависимости от размеров генеральной совокупности и целей исследования выделяют:

- метод сплошного обследования (изучение всех единиц генеральной совокупности) – наиболее точен, но трудоемкий;

- метод выборочного обследования (выборочная совокупность – часть генеральной совокупности, носящая ее характеристики) – менее точен, нетрудоемкий.

3. Определение процедуры формирования выборки. Процедура формирования выборки – это последовательность отбора респондентов в выборку. Выделяют случайные и неслучайные процедуры формирования выборки.

Если все единицы выборки имеют известный шанс (вероятность) быть включенными в нее, то выборка называется вероятностной (случайной). Если этот шанс (вероятность) неизвестен, то выборка называется невероятностной (неслучайной).

Случайные выборки:

- простая;

- систематическая;

- кластерная;

- стратифициованная.

Простая выборка предполагает, что вероятность включения в выборку известна, одинакова для всех единиц совокупности и определяется соотношением объема выборки к размеру совокупности. Данный отбор может осуществляться с помощью формирования выборки вслепую и таблицы случайных чисел. В таких таблицах содержатся числа, порядок включения которых осуществлен случайным образом. Единицам генеральной совокупности присваивают порядковые номера, выбирают любую начальную точку и, двигаясь в произвольном направлении, меняя направление движения, выбирают необходимое количество номеров из числа присвоенных, равное заранее установленному объему выборки. Использование простого случайного отбора гарантирует, что каждая единица совокупности известна и имеет равные шансы быть включенной в выборку.

Систематическая (механическая) выборка. Первый элемент выбирается с помощью таблицы случайных чисел. Остальные элементы выборки отбираются через равные интервалы (выборочные интервал), которые равны отношению объема генеральной совокупности к объему выборки. Если генеральная совокупность упорядочена по признаку, значимому для исследования, то единицы выборки следует отбирать из середины установленного интервала.

Кластерная выборка, основанная на делении совокупности на подгруппы (кластеры), каждая из которых представляет совокупность в целом. Предположим, что исследуется мнение населения региона относительно уровня оказания определенного вида услуг. Регион разбивается на четко определяемые части (кластеры), например районы. Исследователь может считать, что выделенные кластеры идентичны и мнение населения этих районов характерно для региона в целом. Далее несколько районов (кластеров) выбирается случайным образом, выявляется совокупность для этой области, в них проводится исследование, а выводы обобщаются и распространяются на весь регион.

В случае использования стратифицированной выборки генеральная совокупность может быть разделена на несколько групп (страт) с набором определенных признаков. Далее общий размер всей выборки распределяется по отдельным стратам в соответствии с удельным весом каждой страты в генеральной совокупности. Затем для каждой страты с помощью случайного отбора формируется выборка. Используется при телефонном опросе.

Неслучайные выборки:

- произвольная;

- типовая;

- квотированная.

При использовании произвольной выборки элементы выбираются без опеделенного плана или системы. Главный принцип – удобство. Метод недорог.

Типовая выборка ограничивается лишь характерными (типичными) элементами генеральной совокупности, используется при формировании фокус-групп.

При использовании квотированной выборки структура выборки строится так же, как и генеральная совокупость. От каждой группы генеральной совокупности отбираются участники исследования, количество которых пропорционально представительству группы в генеральной совокупности. Используется при личном опосе.

В реальности решение об объеме выборки является компромиссом между теоретическими предположениями о точности результатов обследования и возможностями их практической реализации, прежде всего имеются в виду затраты на проведение опроса. На практике используются несколько подходов к определению объема выборки, приведем наиболее распространенные.

1. Произвольный метод расчета. Объем выборки определяется на уровне 5-10% от генеральной совокупности. Данный подход является простым и легким в исполнении, однако не представляется возможным установить точность и надежность полученных результатов. При достаточно большой совокупности он к тому же может быть и весьма затратным.

2. Традиционный метод расчета. Связан с проведением периодических ежегодных исследований, охватывающих, например, 500, 1000 или 1500 респондентов. Объем выборки может быть установлен исходя из неких заранее оговоренных условий. Допустим опрос 150 потребителей определенного вида услуг дает результат с ошибкой не более 5%. Заказчик маркетингового исследования рекомендует исследователю придерживаться данной цифры.

3. Затратный метод. Основывается на размере затрат на исследование. В ряде случаев в качестве основного аргумента при определении объема выборки используется стоимость маркетингового исследования. Так, в бюджете маркетинга компании предусмотрена конкретная сумма на проведение маркетинговых исследований, которая не подлежит последующей корректировке. Объективность получаемой информации, как правило, в расчет не принимается.

4. Статистический метод расчета, наиболее точный. Объем выборки может определяться на основе статистического анализа. Этот подход основан на выявлении минимального объема выборки исходя из определенных требований к надежности и достоверности получаемых данных. Он также используется при анализе результатов для отдельных подгрупп, формируемых в составе выборки по полу, возрасту, уровню образования и т. п. Требования к надежности и точности результатов для отдельных подгрупп диктуют определенные требования к объему выборки в целом.

При статистическом методе объем выборки n определяется по формуле:

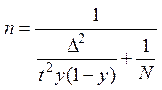где n – численность выборки;

N – объем генеральной совокупности;

t – коэффициент соответствия доверительной вероятности;

∆ – допустимая ошибка;

y – доля исследуемого признака в генеральной совокупности.

При вероятности 0,990 значение коэффициента t равно 3,0, а при вероятности 0,999 – 3,28. Чаще всего при расчетах опираются на вероятность 0,954, при которой t = 2.

Дисперсию обычно определяют на основе эксперимента, пробного исследования или же по аналогам. Так как выборка возрастает при увеличении доли исследуемого признака в генеральной совокупности, то при неизвестных значениях этой доли следует брать y, равный 50 %. При этом формула упрощается до следующего вида:

n = ------------------------------,

∆²+ 1/ N

Зависимость размера выборки от величины генеральной совокупности