Две плоскости в пространстве могут пересекаться по собственной и несобственной прямой, следовательно они могут пересекаться или быть параллельными.
4. Параллельность плоскостей.
Из элементарной геометрии известна теорема (признак параллельности плоскостей):
Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Следствие: если плоскости заданы следами и одноименные следы плоскостей параллельны, то и плоскости параллельны.
(QH PH)
PH)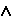 (QV
(QV PV)
PV)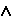 (QW
(QW PW)
PW)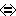 Q
Q P
P
Из этого соотношения следует, что если хотя бы одна пара одноименных следов пересекается, то и плоскости пересекаются.
Из этих определений легко вывести способ построения параллельных плоскостей на чертеже.
Пример: Через точку А провести плоскость, параллельно заданной.
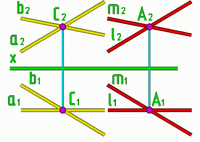 Рис.9
Рис.9
| l2 a2 l1 a2 l1 a1 m2 a1 m2 b2 m1 b2 m1 b1 b1
|
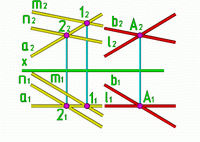 Рис.10
Рис.10
| b2 m2 b1 m2 b1 m1 l2 m1 l2 a2 l1 a2 l1 a1 a1
|
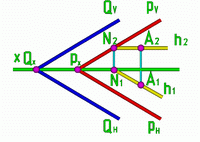 Рис.11
Рис.11
| h2 X h1 X h1 QH QH QH QH PH PH
|
h1 QH, так как QH
QH, так как QH PH (и вообще P
PH (и вообще P Q по условию).
Q по условию).
Для плоскостей общего положения (QH PH)
PH) (QV
(QV PV)
PV) (QW
(QW PW)
PW)
Условие параллельности QW и PW проверяется построением.
5. Пересечение плоскостей.
Две плоскости пересекаются по прямой линии, следовательно для определения линии пересечения достаточно найти
а) две точки, принадлежащие одновременно каждой из двух заданных плоскостей;
б) одну точку, если известно направление линии пересечения.
 2014-01-25
2014-01-25 730
730








