Определение видимости на эпюрах.
При пересечении прямой с плоскостью для улучшения наглядности чертежа для показа видимых линий применяют сплошные основные линии, для невидимых линий - штриховые. При показе видимости линий на эпюре предполагается, что:
o Плоскости и поверхности непрозрачные.
o Наблюдатель всегда находится в первой четверти или первой октанте.
o Луч зрения от наблюдателя перпендикулярен к той или иной плоскости проекций (по отношению к которой определяется видимость).
Точки, относящиеся к различным геометрическим объектам и лежащие на одном проецирующем луче, называются конкурирующими в видимости по отношению к той плоскости проекций, к которой проецирующий луч перпендикулярен.
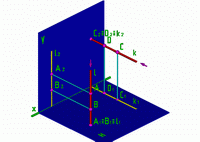 Рис.3
Рис.3
|
Если точка А и точка В лежат на одном проецирующем луче l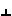 H, то есть A
H, то есть A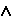 B
B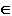 l
l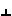 H, то точки А и В называются конкурирующими в видимости по отношению к плоскости H. Причем точка А видимая. Она заслоняет точку В. Точка В невидимая.
H, то точки А и В называются конкурирующими в видимости по отношению к плоскости H. Причем точка А видимая. Она заслоняет точку В. Точка В невидимая.
Аналогично, С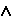 D
D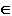 k
k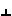 V. С - видимая. D - невидимая.
V. С - видимая. D - невидимая.
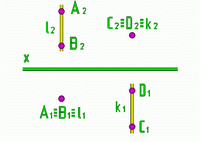 Рис.4
Рис.4
|
На эпюре из двух конкурирующих точек будет видима та проекция, которая дальше отстоит от плоскости проекций, по отношению к которой они конкурируют.
Рассмотрим общий случай: Плоскость и пересекающая ее прямая произвольно расположены в пространстве.
Для нахождения точки встречи прямой с плоскостью в этом случае нужно:
o Через прямую m провести вспомогательную плоскость S; m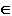 S
S
o Построить прямую пересечения l плоскостей 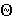 и S; l=
и S; l=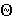
 S.
S.
o Построить точку пересечения К - точку встречи, как результат пересечения прямых l и m. K=l m.
m.
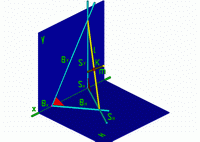 Рис.5
Рис.5
|
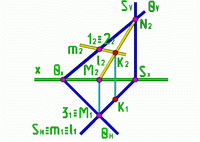 Рис.6
Рис.6
| 12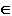 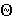 V 22 V 22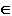 m2 M1 m2 M1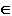  H 31 H 31 m1 m1
|
При определении видимости на плоскость Н рассматриваем проекции конкурирующих точек на плоскость V, а при определении видимости на плоскость V рассматриваем проекции конкурирующих точек на плоскости Н.
Пример. Определить точку встречи прямой m и плоскости Р, заданной треугольником АВС.
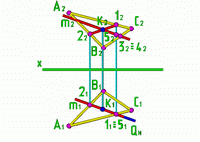 Рис.7
Рис.7
| 32 m2 42 m2 42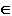 [B2C 2] 11 [B2C 2] 11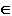 [A1C1] 51 [A1C1] 51 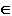 m1 m1
|
 2014-01-25
2014-01-25 942
942








