Прямая и плоскость в пространстве могут иметь одну собственную или несобственную общую точку или множество общих точек, следовательно, прямая может пересекаться с плоскостью, быть ей параллельна либо совпадать с плоскостью.
6. Параллельность прямой и плоскости.
Из элементарной геометрии известно, что прямая параллельна плоскости, если в плоскости можно провести прямую, параллельную заданной прямой.
(m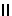 n)
n)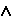 (n
(n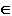
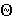 )
)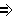 m
m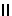
Через точку, не принадлежащую плоскости, можно провести бесконечное количество прямых, параллельных плоскости. Для получения единственного решения нужно наложить дополнительное условие, например, построить прямую, параллельную сразу двум плоскостям.
Пример 1: Через точку А провести прямую l, параллельную заданной плоскости 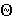 .
.
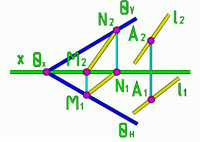 Рис.1
Рис.1
| l2 N2M2 l1 N2M2 l1 M1N1 M1N1
|
Пример 2: Через точку А провести прямую, параллельную заданной плоскости и плоскости проекций V.
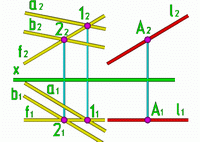 Рис.2
Рис.2
| l2 f2 l1 f2 l1 f1 f1
|
7. Пересечение прямой с плоскостью.
Определение точки встречи прямой с плоскостью относится к элементарным задачам начертательной геометрии, но значение этой задачи большое, так как эта задача входит составной частью в решение многих других позиционных и метрических задач.
Метрические задачи - задачи, в которых определяют размеры геометрических элементов и расстояния между ними.
 2014-01-25
2014-01-25 811
811








