Если функциональный ряд 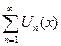 на [a;b] мажорируется сходящимся числовым рядом
на [a;b] мажорируется сходящимся числовым рядом 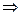
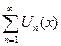 равномерно сходится на этом отрезке.
равномерно сходится на этом отрезке.
Свойства равномерно сходящегося функционального ряда:
Теорема 1: Если функциональный ряд 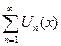 ,составленный из непрерывных функций на [a;b], равномерно сходится на этом отрезке, то сумма ряда S(x) – тоже будет непрерывной функцией на [a;b].
,составленный из непрерывных функций на [a;b], равномерно сходится на этом отрезке, то сумма ряда S(x) – тоже будет непрерывной функцией на [a;b].
Рассмотрим функциональный ряд 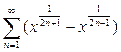
Этот ряд состоит из непрерывных степенных функций, n частичная сумма ряда 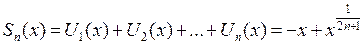
Вычислим сумму ряда:
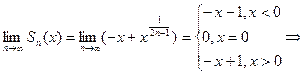
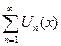 - сходится, но S(x) – является разрывной функцией.
- сходится, но S(x) – является разрывной функцией.
Вывод: S(x) не сходится равномерно.
Теорема 2: Если функциональный 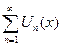 равномерно сходится на [a;b]
равномерно сходится на [a;b] 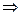 его можно почленно интегрировать на любом отрезке входящем в [a;b] условием интегрируемости является непрерывность функции
его можно почленно интегрировать на любом отрезке входящем в [a;b] условием интегрируемости является непрерывность функции 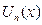 .
.
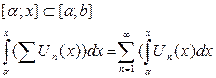
Пример:
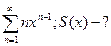
Теорема 3: Если функциональный 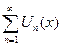 равномерно сходится на [a;b] и ряд составленный из производных
равномерно сходится на [a;b] и ряд составленный из производных 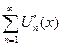 тоже равномерно сходится на [a;b]
тоже равномерно сходится на [a;b]  функциональный ряд можно почленно дифференцировать.
функциональный ряд можно почленно дифференцировать.
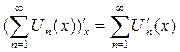
Пример:
 2014-01-25
2014-01-25 724
724








