2014-01-25
706
Степенной ряд по степеням х-а
Рассмотрим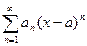 
Сделаем замену: x-a=X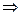
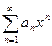
Найдём интервал сходимости полученного ряда, -R<x<R, сделаем обратную замену: -R<x-a<R|+a, 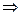a-R<x<a+R
Интервал сходимости полученного ряда имеет центр в точке А.
Пример:
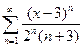
На I курсе рассматривалась формула Тейлора для функции f(x) n+1 раз дифференцируемая в окрестности точки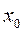 
.
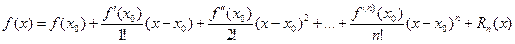
где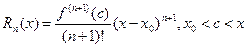 
Если f(x) любое число раз дифференцируема в окрестности точки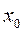 
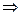
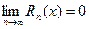переходя к пределу 
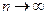в формуле Тейлора получим:
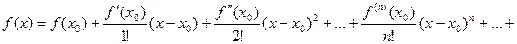
ряд стоящий в правой части равенства называется рядом Тейлора для функции f(x) по степеням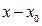 
, а сама формула называется разложением функции f(x) в ряд Тейлора.
Формально ряд Тейлора может быть получен для любой функции, но сходится к этой функции он будет только тогда, когда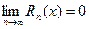
Если этот предел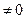 
, то ряд либо расходится, либо сходится к совсем другой функции.
