Тригонометрическим рядом Фурье для функции f(x) на интервале от 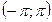
называется ряд вида:
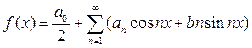 , где
, где
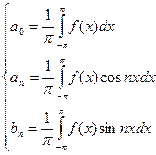
Условия разложимости:
Пусть f(x):
1) Периодическая с 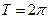
2) Кусочномонотонна
3) Ограничена на 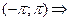 функцию f(x) можно разложить в ряд Фурье на
функцию f(x) можно разложить в ряд Фурье на 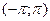 , который сходится к этой функции во всех точках непрерывности, в точках разрыва сумма ряда равна полусумме левого и правого предела функции.
, который сходится к этой функции во всех точках непрерывности, в точках разрыва сумма ряда равна полусумме левого и правого предела функции.
Замечание: Основная трудность построения рядов Фурье в вычислении интегралов.
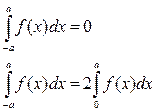
Пример:
Разложить функцию f(x)=x на 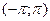 в тригонометрический ряд Фурье, сделать чертеж.
в тригонометрический ряд Фурье, сделать чертеж.
Тригонометрический ряд Фурье от четных и нечетных функций и на интервале 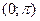
 Если f(x) – четная
Если f(x) – четная 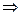
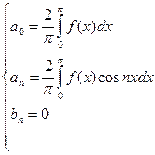
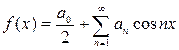 - ряд Фурье по косинусам.
- ряд Фурье по косинусам.
Если f(x) – нечетная 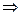
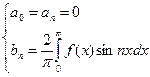

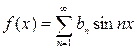 - ряд Фурье по синусам.
- ряд Фурье по синусам.
Если функция f(x) определена на интервале 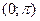 ее нужно продолжить (доопределить) на интервал
ее нужно продолжить (доопределить) на интервал 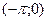 и только потом построить ряд Фурье. Продолжение функции на интервал
и только потом построить ряд Фурье. Продолжение функции на интервал 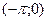 должно быть естественным, лучшее продолжение – четное или нечетное.
должно быть естественным, лучшее продолжение – четное или нечетное.
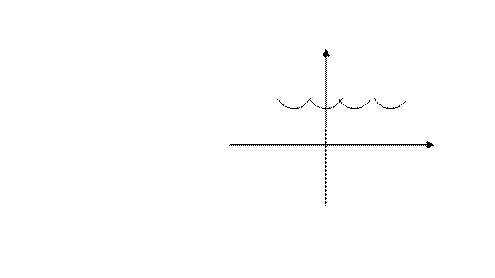
Четное продолжение:
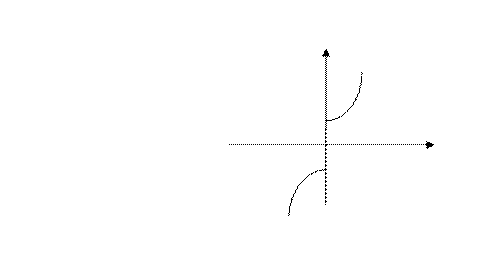
Нечетное продолжение:
Пример:
Разложить функцию f(x)=1 на 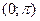 в тригонометрический ряд Фурье продолжив её на
в тригонометрический ряд Фурье продолжив её на 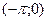 нечетным образом.
нечетным образом.
Тригонометрический ряд Фурье на интервале 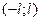
Пусть f(x) определена на 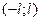 и период
и период 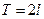
Замена: 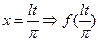 определена на
определена на 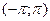 и с периодом
и с периодом 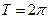 и ее можно разложить в тригонометрический ряд Фурье:
и ее можно разложить в тригонометрический ряд Фурье:
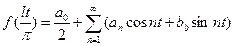 , где
, где 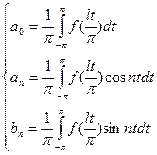
Замена: 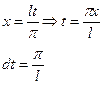
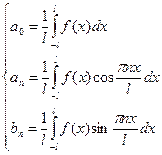
| t | 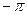
| 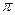
|
| x | 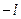
| 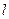
|

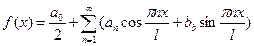 - тригонометрический ряд Фурье по на
- тригонометрический ряд Фурье по на 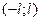
Условия разложимости функции в ряд Фурье на интервале 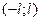 аналогично условиям на интервале
аналогично условиям на интервале 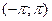
Пример:
f(x)=2x+3 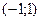 разложить в ряд Фурье
разложить в ряд Фурье
Ряды Фурье на интервале 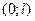
Если f(x) кусочно-монотонна и ограничена на интервале 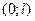 , то её нужно продолжить на интервал
, то её нужно продолжить на интервал 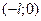 либо чётным, либо нечётным образом.
либо чётным, либо нечётным образом.
Для чётного продолжения:

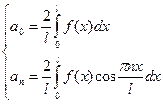
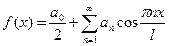
Для нечетного продолжения:

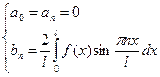
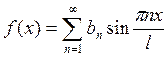
 2014-01-25
2014-01-25 843
843








