Векторное произведение векторов

1. Определение. Векторным произведением a´b неколлинеарных векторов а и b называется вектор, удовлетворяющий трем условиям:

(ВП1) Вектор a´b ортогонален векторам а и b.

(ВП2) | a´b | = |а||b|sinÐ(a,b).

(ВП3) Базис (a,b, a´b) векторного пространства V₃ положительно ориентирован.

Векторное произведение коллинеарных векторов по определению полагают равным нулевому вектору. Проверьте, что условия (ВП1) и (ВП2) выполняются и в этом случае.

Замечания. (8.1) Условие (ВП3) показывает, что векторное произведение, как и смешанное, имеет смысл только в ориентированном трехмерном векторном пространстве.

(8.2) Отложим от произвольной точки А векторы АВ = а и AD = b, достроим треугольник ABD до параллелограмма ABCD и заметим, что площадь этого параллелограмма равна |АВ||АD|sinÐBAD = |а||b|sinÐ(a,b). Таким образом, условие (ВП2) имеет простой геометрический смысл: модуль векторного произведения численно равен площади параллелограмма, построенного на векторах-сомножителях.

(8.3) Векторное произведение равно 0 тогда и только тогда, когда сомножители коллинеарны. "Тогда" здесь следует прямо из определения, а "только тогда" – из 8.2: ведь если векторы неколлинеарны, то площадь построенного на них параллелограмма отлична от 0.

Покажем, как построить векторное произведение двух данных неколлинеарных векторов. Для этого снова построим параллелограмм ABCD, у которого АВ = а и AD = b, и проведем через точку А прямую т перпендикулярно плоскости АВС. На этой прямой от точки А отложим отрезки AE и AF, длиной |а||b|sinÐ(a,b) (рис.30). В силу условий (ВП1) и (ВП2) вектор a´b должен совпадать с AE или AF. Поскольку AE = –AF, базисы (а, b, АЕ) и (а, b, АF) противоположно ориентированы (упражнение 6.6). Поэтому ровно один из этих базисов ориентирован положительно. Входящий в него вектор (AE или AF) и будет единственным, удовлетворяющим все трем условиям (ВП1)-(ВП3). Таким образом у любых двух векторов есть векторное произведение, и притом только одно.

2. Связь скалярного, векторного и смешанного произведений.

(8.4) Теорема. Для любых векторов а, b и с выполняется равенство abc = (a´b)c. Подробнее: смешанное произведение трех векторов равно векторному произведению двух первых векторов, скалярно умноженному на третий вектор.

ÿ Если векторы а и b коллинеарны, то abc = 0 в силу компланарности векторов а, b и с, а (a´b)c = 0, поскольку a´b = 0. Если векторы а и b неколлинеарны, а вектор с компланарен с ними, то abc = 0 и (a´b)c = 0, поскольку вектор a´b перпендикулярен плоскости, которой параллельны векторы а, b и с. Таким образом, в этих двух случаях теорема справедлива.

Если векторы а, b и с некомпланарны, разложим вектор с по базису (а, b, a´b):
с = xa + yb + z(a´b). Поскольку a´b ^ а и a´b ^ b, имеем:

(a´b)c = (a´b)(xa + yb + z(a´b)) = x(a´b)a + y(a´b)b + z(a´b)(a´b) = z(a´b)² (*).

Построим прямой параллелепипед АВСDА₁В₁C₁D₁, у которого АВ = а, AD = b и АА₁ = a´b. Базис (а, b, a´b) по определению положительно ориентирован. Поэтому смешанное произведение ab(a´b) положительно. Но тогда

ab(a´b) = 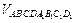= 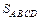·|АА₁| = |a´b||a´b| = |a´b|² = (a´b)²,

откуда

abc = ab(xa + yb + z(a´b)) = хaba + yabb + z ab(a´b) = z(a´b)² (**),

ибо aba = abb = 0 в силу компланарности сомножителей.

Сравнивая равенства (*) и (**), получаем требуемый результат. ÿ

3. Выражение векторного произведения в координатах и его алгебраические свойства.

(8.5) Теорема. Пусть в некотором положительно ориентированном ортонормированном базисе пространства V₃ заданы векторы а(а₁, а₂, а₃) и b(b₁, b₂, b₃). Тогда вектор a´b имеет в этом базисе координаты

(, –, ).

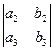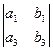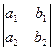ÿ Пусть в данном базисе a´b(x,y,z). По формуле 5.14, теореме 8.4 и свойству 7.9 имеем:

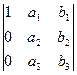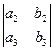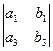х = (a´b)i = abi = – aib = iab = = 1– 0+ 0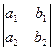= 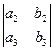. Аналогично (как?) y = jab = –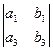, a z = kab = 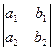. ÿ

Теперь нетрудно доказать другие алгебраические свойства векторного произведения:

(8.6) a´b = – b´a (антикоммутативность).

(8.7) (а₁+а₂)´b = a₁´b + a₂´b и a´(b₁+b₂) = a´b₁ + a´b₂ (дистрибутивность).

(8.8) (хa)´b = a´(xb) = х(a´b) (однородность).

ÿ Проверим, например, антикоммутативность. По теореме 8.5

a´b(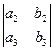, –, 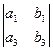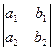) = (a₂b₃–a₃b₂, a₃b₁–a₁b₃, a₁b₂–a₂b₁).

По той же теореме

b´a(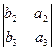, –, 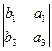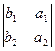) = (a₃b₂ – a₂b₃, a₁b₃ – a₃b₁, a₂b₁ – a₁b₂) = –a´b. ÿ

Вычисления, проверяющие свойства 8.7 и 8.8, проведите сами.

4. Площади параллелограмма и треугольника. Возьмем произвольный треугольник АВD и достроим его до параллелограмма ABCD. В силу замечания 8.2 площадь параллелограмма ABCD равна модулю векторного произведения АВ´AD:

(8.9) 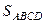= |AB´AD|.

Площадь параллелограмма ABCD вдвое больше площади треугольника АВD. Поэтому

(8.10) 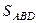= 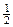|AB´AD|.

Полученные формулы в соединении теоремой 8.5 позволяют находить площадь параллелограмма или треугольника по известным координатам векторов его сторон (базис при этом, разумеется, должен быть ортонормированным).

(8.11) Упражнение. Выведите соответствующие координатные формулы.