1. Определение и простейшие свойства. В отличие от чисел, у векторов существует не одно, а несколько разных “умножений”. Мы уже рассматривали скалярное умножение векторов. В этом параграфе мы познакомимся еще с одним, в котором участвуют не два, как обычно, а сразу три сомножителя.
Пусть V3 – ориентированное трехмерное векторное пространство, B = (i,j,k) – его положительно ориентированный ортонормированный базис. Смешанным [10] произведением abc векторов a, b и с называется определитель перехода DB ®(a,b,с). Подробнее, если в базисе B а(а1,а2,а3), b(b1,b2,b3), с(с1,с2,с3), то по определению
(7.1) abc = 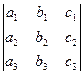 .
.
Прямо из определения смешанного произведения вытекают такие его свойства:
(7.2) abc = 0 тогда и только тогда, когда векторы a, b и с компланарны.
(7.3) Смешанное произведение abc положительно (отрицательно) тогда и только тогда, когда базис (a,b,c) положительно (отрицательно) ориентирован.
Для доказательства других свойств нам понадобится
(7.4) Лемма. Определитель перехода от одного ортонормированного базиса пространства V3 к другому равен 1, если эти базисы одинаково ориентированы, и –1, если они противоположно ориентированы.
ÿ Пусть B = (i,j,k) и D = (i¢,j¢,k¢) – два ортонормированных базиса пространства V3. Положим а1 = cosÐ(i,i¢) = cosÐ(i¢,i), а2 = cosÐ(i,j¢) = cosÐ(j¢,i), а3 = cosÐ(i,k¢) = cosÐ(k¢,i), b1 = cosÐ(j,i¢) = cosÐ(i¢,j), b2 = cosÐ(j,j¢) = cosÐ(j¢,j), b3 = cosÐ(j,k¢) = cosÐ(k¢,j), c1 = cosÐ(k,i¢) = cosÐ(i¢,k), c2 = cosÐ(k,j¢) = cosÐ(j¢,k), c3 = cosÐ(k,k¢) = cosÐ(k,k¢). Тогда в силу (5.16) векторы базиса B в базисе D имеют координаты i(а1,а2,а3), j(b1,b2,b3), k(с1,с2,с3), а векторы базиса D в базисе B – координаты i¢(а1,b1,c1), j¢(a2,b2,c2), k¢(a3,b3,с3). Отсюда получаем:
DD ®B = 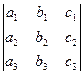 , DB ®D =
, DB ®D = 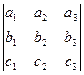 .
.
Расписывая получившиеся определители по формуле (6.4) (сделайте это!), находим, что они равны. С другой стороны, согласно (П3), DB ®D = 1/DD ®B. Получается, что DB ®D = 1/DB ®D, откуда (DB ®D)2 = 1. Значит DB ®D = 1 или DB ®D = –1. ÿ
(7.5) Следствие. Смешанное произведение не зависит от выбора положительно ориентированного базиса B. При смене ориентации пространства смешанное произведение меняет знак.
ÿ В самом деле, если B и D – два положительно ориентированных базиса пространства V3, то в силу леммы DB®(a,b,с) = DB®DDD®(a,b,с) = 1´DD®(a,b,с) = DD®(a,b,с). Если бы базис D ориентирован отрицательно, то DB®D = –1 и DD ®(a,b,с) = –DB ®(a,b,с). ð
Допустим теперь, что D = (е1, е2, е3) – произвольный базис пространства V3, а векторы а(х1,х2,х3), b(y1,y2,y3), с(z1,z2,z3) заданы своими координатами в нем. Тогда по определению abc = DB ®(a,b,с) = DB ®DDD ®(a,b,с) = (е1е2е3)DD®(a,b,с). Расписывая DD ®(a,b,с) как определитель, получаем еще одно полезное свойство:
(7.6) Если векторы а(х1,х2,х3), b(y1,y2,y3), с(z1,z2,z3) заданы своими координатами в произвольном базисе D = (е1, е2, е3), то abc = (е1е2е3)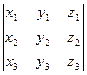 . ÿ
. ÿ
2. Алгебраические свойства смешанного произведения.
(7.7) Смешанное произведение дистрибутивно по каждому из сомножителей:
(а1+а2)bc = а1bc + а2bc, а(b1+b2) c = аb1 c + аb2c, аb(c1+c2) = аbc1 + аbc2.
(7.8) Смешанное произведение однородно по каждому из сомножителей:
(xa)bc = a(xb)c = ab(xc) = x(abc).
(7.9) При перестановке двух сомножителей смешанное произведение меняет знак:
bac = acb = cba = –abc (антикоммутативность).
ÿ Все эти свойства доказываются прямым вычислением. Проверим, например, равенство (xa)bc = x(abc). Пусть в некотором положительно ориентированном ортонормированном базисе а(а1,а2,а3), b(b1,b2,b3), с(с1,с2,с3). Тогда
(xa)bc = 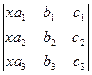 = (ха1)b2c3 – (xа1)b3c2 + b1c2(xа3) – b1c3(xa2) + c1 (xа2)b3 + c1(xа3)b2 = х(а1b2c3 – а1b3c2 + b1c2а3 – b1c3a2 + c1а2b3 + c1а3b2) = х
= (ха1)b2c3 – (xа1)b3c2 + b1c2(xа3) – b1c3(xa2) + c1 (xа2)b3 + c1(xа3)b2 = х(а1b2c3 – а1b3c2 + b1c2а3 – b1c3a2 + c1а2b3 + c1а3b2) = х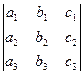 = х(abc). Остальные свойства проверьте сами. ÿ
= х(abc). Остальные свойства проверьте сами. ÿ
3. Смешанное произведение как объем.
(7.10) Теорема. Объем параллелепипеда АВСDА1В1C1D1 равен абсолютной величине смешанного произведения векторов АВ, АD и АА1.
ÿ Опустим из вершины А перпендикуляры АК на прямую СD и АН на плоскость А1В1C1. Положим i = АВ/|АВ|, j = АK/|АK| и k = АH/|АH|. В силу (2.10) i, j и k – единичные векторы, сонаправленные соответственно векторам АВ, АК и АН (рис.28).
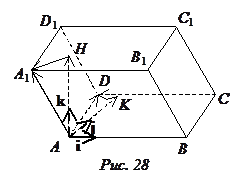 По построению АВ = |АВ| i, АD = AK + KD = |AK| j+xi, AA1 = AH + HA1 =
По построению АВ = |АВ| i, АD = AK + KD = |AK| j+xi, AA1 = AH + HA1 =
|AH| k + yi + zj. Здесь KD = xi, ибо KD || i, а HA1 = yi + zj, так как вектор HA1 компланарен неколлинеарным векторам i и j. Таким образом, в базисе (i,j,k) векторы АВ, АD и АА1 имеют такие координаты: АВ(|АВ|, 0, 0), АD(х, |АК|, 0), AA1(y, z, |AН|). Составленный из них определитель D равен |АВ| |АК| |АН| (проверьте!). Поскольку |АВ| |АК| – это площадь параллелограмма ABCD, а |АН| – высота параллелепипеда АВСDА1В1C1D1, определитель D равен объему этого параллелепипеда.
Заметим теперь, что по построению базис (i,j,k) – ортонормированный. Если он положительно ориентирован, то по определению АВ АD АА1 = D, а если отрицательно, то по следствию 7.5 АВ АD АА1 = –D. В обоих случаях |АВ АD АА1| = |D| = D. ÿ
(7.11) Следствие. Объем тетраэдра ABDA1 равен 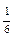 |АВ АD АА1|.
|АВ АD АА1|.
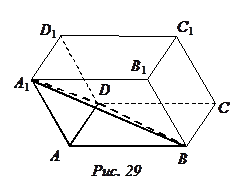 ÿ Достроим тетраэдр ABDA1 до параллелепипеда АВСDА1В1C1D1 (рис.29). Объем тетраэдра равен трети произведения площади треугольника ABD на высоту АН, что составляет 1/6 объема параллелепипеда. ÿ
ÿ Достроим тетраэдр ABDA1 до параллелепипеда АВСDА1В1C1D1 (рис.29). Объем тетраэдра равен трети произведения площади треугольника ABD на высоту АН, что составляет 1/6 объема параллелепипеда. ÿ
Посмотрим, как работают эти утверждения.
Задача. Найти отношение объема параллелепипеда АВСDА1В1C1D1 к объему тетраэдра ACB1D1.
ÿ Рассмотрим в пространстве V3 базис (АВ, АD, АА1). В нем АС(1,1,0), AB1(1,0,1), AD1(0,1,1). По свойству 7.6 АС AB1 АD1 = (АВ АD АА1)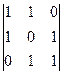 = –2(АВ АD АА1). По теоремам 7.10 и 7.11
= –2(АВ АD АА1). По теоремам 7.10 и 7.11 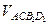 =
= 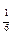 |АС AB1 АD1| =
|АС AB1 АD1| = 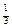 |АВ АD АА1| =
|АВ АD АА1| = 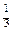
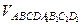 .Ответ: 1/3. ÿ
.Ответ: 1/3. ÿ
 2014-01-25
2014-01-25 828
828








