Деление отрезка в данном отношении

1. Определение и примеры. Пусть точка С лежит на прямой (АВ) и не совпадает с точкой В. Тогда векторы AC и СВ коллинеарны, причем СВ ¹ 0, и, следовательно, существует единственное число l, для которого АС = lСВ. Это число называется отношением, в котором точка С делит отрезок [АВ], или простым отношением точек А, В и С [12] и обозначается (АВ,С). Из данного определения и признака 2.12 следует, что

(10.1) (АВ,С) = .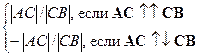

Если точка С лежит на отрезке [АВ], то АС­­СВ и наше определение совпадает со школьным.

(10.2) Примеры. Середина отрезка делит его в отношении 1. Точка пересечения медиан делит каждую из них в отношении 2 (считая от соответствующей вершины). Если С₁ и С₂ – основания биссектрис соответственно внутреннего и внешнего углов при вершине С треугольника АВС, то (АВ,С₁) = |СА|/|СВ| и (АВ,С₂) = –|СА|/|СВ|. Доказательства проведите самостоятельно.

2. Свойства. (10.3) Простое отношение трех точек не может равняться –1. Для каждого l ¹ –1 существует единственная точка, делящая отрезок [АВ] в отношении l.

ð Заметим, что l = (АВ,С) Û АС = lСВ Û АС = l(АС – АВ) Û (1+l)АС = lАВ. Равенство (1+l)АС = lАВ при l = –1 превращается в неверное: 0 = –АВ. Поэтому никакая точка не может делить отрезок в отношении –1. Если же l ¹ –1, то, деля обе части равенств (1+l)АС = lАВ на 1+l, получаем, что l = (АВ,С) тогда и только тогда, когда

(10.4) АС = 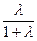АВ.

Равенство (10.4) однозначно задает точку С, что доказывает второе утверждение (10.3). ð

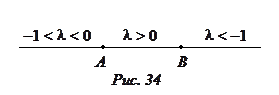Если точка С, отличная от А и В, лежит на отрезке [АВ] то АС­­СВ, и (АВ,С) = |AC|/|CB| > 0. Если точка С лежит за точкой А, то АС­¯СВ и |AC| < |CB|, откуда –1< (АВ,С) = –|AC|/|CB| < 0. Если точка С лежит за точкой В, то АС­¯СВ и |AC| > |CB|, откуда (АВ,С) = –|AC|/|CB| < –1. Этим доказано, что

(10.5) трем промежуткам, на которые точки А и В разбивают прямую (АВ), соответствуют значения простого отношения l, указанные на рис. 34. ð

3. Выражение в координатах. Возьмем в некоторой АСК в пространстве такие точки А(х_А, у_А, z_A), В(х_В, у_В, z_B), С(х_С, у_С, z_C), что точка С лежит на прямой (АВ) и не совпадает с точкой В.

(10.6) Задача. Выразить в координатах отношение l = (АВ,С).

ð Запишем определение (10.1) в координатах:

(10.7) .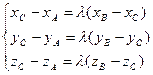

Из (10.7) получаем

(10.8) l = 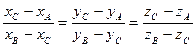. ð

Условие С ¹ В гарантирует, что знаменатель хотя бы одной из дробей в равенстве (10.8) будет отличен от 0. ð

(10.9) Задача. Даны точки А(х_А, у_А, z_A), В(х_В, у_В, z_В) (А ¹ В) и число l, не равное –1. Найти координаты х_С, у_С, z_C точки С, для которой (АВ,С) = l.

ð Из системы (10.7) получаем

(10.10) х_С = 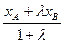, у_С = 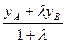, z_С = 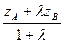. ð

Аналогично мы можем по данным А, С и l (l ¹ 0, l ¹ –1, А ¹ C) однозначно найти точку В, а по известным В, С и l (l ¹ –1, В ¹ C) – точку А (выведите соответствующие формулы сами). Попутно доказана важная

(10.11) Теорема. Из четырех объектов – точек А, В и С и числа l –любые три при соблюдении указанных выше ограничений однозначно определяют четвертый. ð

4. Теорема Фалеса. (10.12) Пусть l и l' – две прямые, лежащие в одной плоскости, а, b и c – три параллельные прямые той же плоскости, пересекающие прямую l в точках А, B и C, а прямую l' – в точках A', B' и C' соответственно. Тогда простые отношения (АВ,С) и (A'B',C') равны.

ð Рассмотрим точки А', B' и С' как проекции точек А, В и С на прямую l' параллельно прямым а, b и c. Поскольку параллельное проектирование сохраняет операции над векторами, имеем: l = (АВ,С) Û АС = lСВ Þ А'С' = lС'В' Û l = (А'В',С'), что и требовалось доказать. ð

Теперь ясно, что теорему Фалеса можно было бы сформулировать и так:

(10.12') Параллельное проектирование сохраняет простое отношение трех точек.

Именно в такой форме она понадобится нам, когда мы будем изучать аффинные отображения и изображения фигур в параллельной проекции.