Различные виды уравнений плоскости

Глава 3. Прямая и плоскость в пространстве.

Плоскость П в пространстве задается своими точкой М₀ и базисной парой, т.е., парой параллельных ей неколлинеарных векторов, образующих базис (a,b) векторной плоскости V₂(П). Если плоскость П задана таким образом, то пишут П = [М₀, a, b].

1. Параметрические уравнения. Пусть дана плоскость П = [М₀, a, b], и в некоторой АСК М₀(х₀,у₀,z₀), a(a₁,a₂,a₃), b(b₁,b₂,b₃). Тогда по теореме 3.10

М(х,у,z)ÎП Û М₀М, а, b компланарны Û

(16.1) М₀М = ua + vb ((u,v)ÎR² ) Û

(16.2)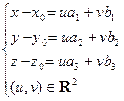

Уравнение (16.1) называется параметрическим уравнением плоскости в векторной форме, а уравнения (16.2) – параметрическими уравнениями плоскости в скалярной форме. Величины u и v называются параметрами, а множество R² – областью определения (изменения) параметров. Если уменьшить область определения, параметрические уравнения будут задавать не всю плоскость, а только какую-то ее часть. Так, взяв в качестве области определения множество {(u,v)ÎR²| 0 £ u,v £ 1}, мы зададим параллелограмм (вместе с внутренними точками), построенный на векторах M₀U = a и M₀V = b.

Отметим, что параметры u и v в уравнениях (16.1)-(16.2) – это координаты точки М в репере (М₀, a, b) на плоскости П. Их называют внутренними координатами точки М, в отличие от ее внешних координат (х,у,z), заданных в пространстве.

2. Каноническое уравнение. Его мы получим, воспользовавшись признаком компланарности (6.5): М(х,у,z)ÎП Û М₀М, а, b компланарны Û

(16.3) 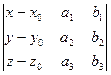= 0.

Уравнение (16.3) и есть каноническое уравнение плоскости в пространстве.

3. Уравнение плоскости, заданной тремя точками. Три неколлинеарные точки М₀(х₀,у₀,z₀), М₁(х₁,у₁,z₁), М₂(х₂,у₂,z₂) однозначно определяют проходящую через них плоскость П = [М₀М₁М₂]. Векторы М₀М₁ и М₀М₁ образуют ее базисную пару. Используя это, запишите самостоятельно ее параметрические и каноническое уравнения.