В этом параграфе, как и в §16, мы работаем исключительно в ПДСК. Для произвольной АСК соответствующие формулы значительно сложнее.
1. Нормальный вектор плоскости – это направляющий вектор перпендикуляра к ней. Равносильным образом его можно определить, как ненулевой вектор, ортогональный всем векторам, параллельным плоскости. Соединяя это с признаком параллельности вектора и плоскости (17.8), получаем, что
(20.1) вектор n(A,B,C) является нормальным для плоскости П: Ax + By + Cz + D = 0.
Поскольку все перпендикуляры к данной плоскости параллельны между собой, все нормальные векторы данной плоскости коллинеарны.
Вывод уравнения плоскости, заданной точкой М0(х0,у0,z0) и нормальным вектором n(A,B,C):
(20.2) A(x–x0) + B(y–y0) + C(z–z0) = 0
копирует вывод уравнения (15.2) для прямых на плоскости. Проделайте его сами.
2. Расстояние от точки до плоскости. Расстояние от точки М1(х1,у1,z1) до плоскости П: Ax + By + Cz + D = 0 находится по формуле
(20.3) d(M1,П) = 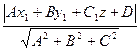 .
.
Доказательство, аналогичное соответствующему рассуждению для прямых на плоскости, проведите самостоятельно.
3. Расстояние от точки до прямой в пространстве. Расстояние от точки М1(х1,у1,z1) до прямой l = [М0(х0,y0,z0), р(a,b,c)] проще всего найти методом площадей. Отложим от точки М0 вектор М0М2 = р и вычислим двумя способами площадь треугольника М0М1М2. С одной стороны, она равна |М0М1´М0М2|/2, с другой – полупроизведению длины |М0М2| = |p| на высоту треугольника, опущенную из вершины М1, то есть на расстояние d(M1,l). Приравнивая эти два выражения, находим, что
(20.4) d(M1,l) = |М0М1´р|/|р|.
4. Другие задачи о расстояниях. Расстояния между параллельными прямыми, параллельными плоскостями, прямой и параллельной ей плоскостью ищутся, как расстояния от некоторой точки первой прямой (плоскости) до второй прямой (плоскости). Интереснее задача о расстоянии между скрещивающимися прямыми, равном, как известно, длине их общего перпендикуляра.
(20.5). Теорема. Если прямые l = [М0(х0,y0,z0), р(a,b,c)] и m = [M1(х1,y1,z1), q(a1,b1,c1)] скрещиваются, то расстояние между находится по формуле
(20.6) d(l,m) = |(М0М1,р,q)|/|р´q|
(в числителе – модуль смешанного произведения).
ð Расстояние между прямыми l и m равно расстоянию от точки М1 до плоскости
П = [М0,р,q)] (А.В. Погорелов. Геометрия 7-11, с 262). Пользуясь этим, докажем формулу (20.6) методом объемов. Отложим от точки М0 векторы М0М2 = р и М0М3 = q. Объем тетраэдра М0М1М2М3 равен |(М0М1,р,q)|/6. С другой стороны, он равен трети произведения высоты тетраэдра, опущенной из вершины М1 (то есть, как раз расстояния от точки М1 до плоскости П) на площадь треугольника М0М2М3, равную |p´q|/2. Приравнивая эти выражения, получаем равенство (20.6). ð
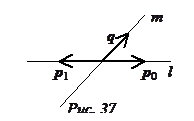 5. Угол между прямыми в пространстве определяется, как наименьший из углов между параллельными им прямыми, проходящими через одну точку. Если взять направляющие векторы данных прямых, то угол между ними будет равен углу между прямыми или смежному с ним (углы между р0 и q и р1 и q соответственно на рис. 37). В первом случае косинусы углов между прямыми и их направляющими векторами равны, во втором – противоположны. При этом угол между прямыми всегда острый или прямой, так что его косинус неотрицателен. Следовательно, этот косинус в любом случае равен модулю косинуса угла между направляющими векторами. Таким образом, угол j между прямыми l = [М0(х0,y0,z0), р(a,b,c)] и m = [M1(х1,y1,z1), q(a1,b1,c1)] находится по формуле:
5. Угол между прямыми в пространстве определяется, как наименьший из углов между параллельными им прямыми, проходящими через одну точку. Если взять направляющие векторы данных прямых, то угол между ними будет равен углу между прямыми или смежному с ним (углы между р0 и q и р1 и q соответственно на рис. 37). В первом случае косинусы углов между прямыми и их направляющими векторами равны, во втором – противоположны. При этом угол между прямыми всегда острый или прямой, так что его косинус неотрицателен. Следовательно, этот косинус в любом случае равен модулю косинуса угла между направляющими векторами. Таким образом, угол j между прямыми l = [М0(х0,y0,z0), р(a,b,c)] и m = [M1(х1,y1,z1), q(a1,b1,c1)] находится по формуле:
(20.7) cosj = |cosÐ(p,q)|.
6. Угол между прямой и плоскостью определяется как угол между прямой и ее ортогональной проекцией на плоскость, если прямая не является перпендикуляром к плоскости, и принимается равным p/2, если является.
Чтобы найти угол j между прямой l = [М0(х0,y0,z0), р(a,b,c)] и плоскостью
П: Ax + By + Cz + D = 0, рассмотрим перпендикуляр n к плоскости. Нетрудно видеть, что угол y между прямыми l и n в сумме с углом j дает p/2. Поэтому, в силу (20.7),
sinj = cosy = |cosÐ(p,n)|, где n(A,B,C) – нормальный вектор плоскости П, откуда
(20.8) sinj = 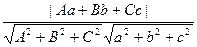 .
.
7. Угол между двумя плоскостями по определению равен величине меньшего из двугранных углов, образованных этими плоскостями, а тот, очевидно, равен углу между перпендикулярами к данным плоскостям. Последний же находится по формуле (20.7), где в качестве векторов p и q берутся нормальные векторы плоскостей П1 и П2. Итак, если плоскости П1 и П2 заданы уравнениями А1х + В1у + С1z + D1 = 0 и
А2х + В2у + С2z + D2 = 0 соответственно, то
(20.9) cosÐ(П1,П2) = |cosÐ(А1,В1,С1),(А2,В2,С2)| = 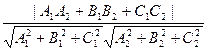 .
.
В частности,
(20.10) П1 ^ П2 Û А1А2 + В1В2 + С1С2 = 0.
[1] Требование, чтобы третий отрезок был ненулевым, существенно: если он нулевой, то утверждение становится просто неверным (почему?).
[2] Конечно, параллелограмм строится не на самих векторах ОА и АС, а на соответствующих направленных отрезках. Ради краткости мы и дальше часто будем называть направленные отрезки “векторами” там, где по общему смыслу сказанного ясно, о чем идет речь.
[3] Здесь и далее под делением вектора на число понимается умножение вектора на число, обратное данному, т.е. под а /| а | понимается (1/| а |) а.
[4] По-гречески орто – прямой, а гониос – угол.
[5] Если, конечно, понимать векторы так, как мы их определили в §1. В курсе алгебры понятие векторного пространства будет значительно обобщено.
[6] Поэтому это произведение и называется скалярным: физики называют скалярными величины, принимающие числовые значения, в отличие от векторных величин, значениями которых являются векторы.
[7] См.: В.Г. Болтянский, “Элементарная геометрия” (М.: ”Просвещение”, 1985) стр. 206-207
[8] Правые и левые базисы можно описать и по-другому. Проведем плоскость (ОАВ) и посмотрим на нее из того полупространства, в которое отложен вектор ОС. Если при этом окажется, что векторы ОА и ОВ задают на плоскости (ОАВ) вращение против часовой стрелки, то базис (ОА, ОВ, ОС) - правый, а если по часовой стрелке – то левый. Это правило используется в физике (в теории электромагнетизма) под названием “правила левой руки”. Есть и другие аналогичные правила – “буравчика” и т.п. Подробнее об этом см. в учебнике “Геометрия” А.Д.Александрова и Н.Ю. Нецветаева (М.: “Наука”, 1990, с. 90-91).
[9] См. упомянутый в предыдущей сноске учебник А.Д.Александрова и Н.Ю. Нецветаева (ч.1, гл.3, §6).
[10] Ибо, как будет показано в §8, оно выражается через скалярное и векторное произведения векторов.
[11] Если точка М лежит в одной из координатных плоскостей, координатный параллелепипед вырождается в параллелограмм, отрезок или точку.
[12] В отличие от сложного отношения четырех точек, изучающегося в проективной геометрии.
[13] Здесь и далее используется радианная мера угла.
[14] Этот факт мы примем без доказательства: его обоснование невозможно без углубления в аксиоматику геометрии, чего мы сейчас не можем себе позволить.
[15] То есть, на некоторое количество полных углов.
[16] Такое соглашение вполне естественно: изучая геометрическую фигуру, неразумно ставить вопрос о том, входят ли в нее слон или Черное море. Какое множество считается универсумом, обычно понятно по смыслу сказанного.
[17] "Уравнением" мы тут для краткости называем любое соотношение между координатами точки, т.е., "уравнение" в нашем смысле может быть и неравенством, и системой и т.д.
[18] Т.е., если одна и та же кривая есть множество корней нескольких многочленов, то ее порядком называется наименьшая из возможных степеней таких многочленов. Например, порядок оси ординат, которую можно задать и уравнением х 2 = 0, и уравнением х = 0, равен 1. Далее, можно показать ([1, с. 52-53]), что если алгебраическая линия есть множество корней некоторого многочлена в одной АСК, то в любой другой АСК она тоже будет множеством корней некоторого (вообще говоря, другого) многочлена той же степени.
[19] Заметим, что в пространстве это уже не так.
[20] В самом деле, плоскости параллельны, когда две пересекающиеся прямые одной из них соответственно параллельны двум пересекающимся прямым другой. Это значит, что есть два неколлинеарных вектора, параллельных обеим плоскостям. Но тогда всякий вектор, параллельный одной из плоскостей, будет линейной комбинацией этих векторов и, значит, будет параллелен и второй плоскости.
 2014-01-25
2014-01-25 1002
1002
