Общее уравнение плоскости

1. Вывод общего уравнения. Сохраняя обозначения, введенные в §16, раскроем определитель в правой части канонического уравнения (16.3):

М(х,у,z)ÎП Û (16.3) Û 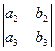(x–x₀) +0 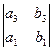(y–y₀) + 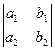(z–z₀) = 0 Û

(17.1) Ax + By +Cz + D = 0,

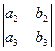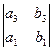где А = , В = , С = 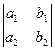, D = –(Ах₀+Ву₀+Сz₀). При этом

(17.2) А² + В² + С² ¹ 0,

ибо иначе уравнение (16.1) задает не плоскость, а пустое множество (при D ¹ 0) или все пространство (при D = 0). Уравнение (17.1) при условии (17.2) называется общим уравнением плоскости (в АСК в пространстве). Мы показали, что

(17.3) всякую плоскость можно задать в данной АСК общим уравнением.

Верен и обратный факт.

(17.4) Теорема. Всякое уравнение вида (17.1) при условии (17.2) задает в данной АСК в пространстве некоторую плоскость.

ð Условие (17.2) означает, что хотя бы один из коэффициентов А, В, С не равен 0. Не умаляя общности, можно считать, что С ¹ 0. Тогда (17.1) Û z = 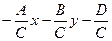Û

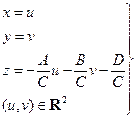. Переписав полученную систему в виде 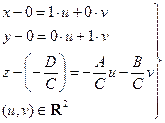, убеждаемся, что это – система параметрических уравнений плоскости, заданной точкой М₀(0, 0, –D/C) и векторами а(1, 0, –А/С), b(0, 1, –B/С). Значит, и равносильное ей уравнение (17.1) задает ту же плоскость. ð

2. Уравнение центральной связки плоскостей. (17.3) Лемма. Пусть точка М₀(х₀,у₀,z₀) лежит в плоскости, заданной уравнением (17.1). Тогда для любых действительных x, y и z выполнено тождество

(17.4) Ax + By + Cz + D = A(x–x₀) + B(y–y₀) + C(z–z₀).

Доказательство аналогично доказательству леммы 14.4. Проведите его сами.

(17.5) Теорема. Если плоскость, заданная уравнением (17.1), проходит через точку М₀(x₀,y₀,z₀), то ее можно задать уравнением

(17.6) A(x–x₀) + B(y–y₀) + C(z–z₀) = 0.

Обратно, всякое уравнение вида (17.6) при условии (17.2) задает некоторую плоскость, проходящую через точку М₀.

ð Первая часть теоремы вытекает из леммы 17.4. Чтобы доказать вторую, заметим, что после раскрытия скобок уравнение (17.6) приводится к виду (17.1), где
D = –(Ax₀+ By₀+ Cz₀). Значит, уравнение (17.6) при условии (17.1) действительно задет плоскость. То, что она проходит через точку М₀, проверяется прямой подстановкой. ð

Центральной связкой плоскостей называется совокупность всех плоскостей, проходящих через данную точку пространства (центр связки). Мы показали, что (17.6) при условии (17.2) есть уравнение связки с центром М₀(х₀,у₀,z₀).

3. Признак параллельности вектора и плоскости. (17.7) Теорема. Вектор р(а,b,c) параллелен плоскости П, заданной общим уравнением (17.1), тогда и только тогда, когда выполнено равенство

(17.8) Aa + Bb + Cc = 0.

ð Отложим от точки М₀(х₀,у₀,z₀)ÎП вектор М₀М = р, и обозначим координаты точки М через (x,y,z) Вектор р параллелен плоскости П тогда и только тогда, когда МÎП, что по теореме (17.5) равносильно равенству A(x–x₀) + B(y–y₀) + C(z–z₀) = 0. Осталось заметить, что по построению x–x₀ = a, y–y₀ = b и z–z₀ = с. ð

(17.9) Следствие. Если плоскость задана в АСК уравнением (17.1), то векторы a(0,–C, B), b(–C,0,A), c(–B,A,0) параллельны этой плоскости.

ð Достаточно подставить координаты данных векторов в равенство (17.8). ð

(17.10) Задача. Записать параметрические уравнения плоскости П: 2х–3у–z+1=0.

ð Достаточно найти точку, лежащую в плоскости и базисную пару векторов. Чтобы найти точку, положим х=у=0 и найдем z = 1, а в качестве базисной пары, согласно следствию (17.9), можно взять векторы (0,1,–3) и (1,0,2). ð

Еще одно следствие проясняет геометрический смысл коэффициентов общего уравнения плоскости.

(17.11) Теорема. Если плоскость П задана уравнением (17.1), то А=0 Û П||Ох, В=0 Û П||Оу, С=0 Û П||Оz, А=В=0 Û П||Оху, А=С=0 Û П||Охz, B=C=0 Û П||Оуz, D=0 Û OÎП.

ð А = 0 Û p(1,0,0) || П Û Ох || П. D = 0 Û 0A + 0B + 0C + D = 0 Û O(0,0,0)ÎП.

А=В=0 Û Ох || П и Оу || П Û Оху || П (по признаку параллельности двух плоскостей). ð

4. Геометрический смысл неравенств первой степени с тремя переменными.

(17.12) Теорема. Каждое из двух неравенств:

и

(17.13+) Ах + Ву + Сz + D > 0

(17.13–) Ах + Ву + Сz + D < 0

задает в АСК в пространстве одно из полупространств, на которые разбивает пространство плоскость П: Ах + Ву + Сz + D = 0.

Доказательство с очевидными изменениями копирует доказательство аналогичной теоремы 14.14. Проведите его самостоятельно.