Общее уравнение прямой на плоскости

1. Вывод общего уравнения. Возьмем прямую l = [М₀(х₀,у₀), l(a,b)] и преобразуем ее каноническое уравнение: (13.4) Û b(x–x₀) = a(y–y₀) Û bx – ay + (ay₀–bx₀) = 0. Если обозначить b через А, –а через В, а ay₀–bx₀ через С, последнее уравнение перепишется в виде

(14.1) Ах + Ву + С = 0,

причем, поскольку вектор l – ненулевой, будет выполнено условие

(14.2) А² + В² ¹ 0.

Уравнение (14.1) при условии (14.2) называется общим уравнением прямой на плоскости.

(14.3) Теорема. Всякую прямую на плоскости можно задать общим уравнением в любой данной АСК. Обратно, всякое уравнение вида (14.1) при условии (14.2) задает в АСК прямую.

(14.4) Лемма. Если пара чисел (х₀,у₀) удовлетворяет уравнению (14.1), то для любых действительных х и у выполнено равенство Ах + Ву + С = А(х–х₀) + В(у–у₀).

ð По условию Ах₀ + Ву₀ + С = 0 Û С = –(Ах₀ + Ву₀). Значит, А(х–х₀) + В(у–у₀) = Ах + Ву – (Ах₀ + Ву₀) = Ах + Ву + С. ð

Доказательство теоремы 14.3. Первое утверждение теоремы доказано при выводе уравнения (14.1). Чтобы доказать второе, сначала покажем, что при условии (14.2) уравнение (14.1) имеет по крайней мере одно решение (х₀,у₀). В самом деле, условие (14.2) означает, что хотя бы одно из чисел А или В отлично от нуля. Допустим, В ¹ 0 (случай А ¹ 0 разбирается аналогично). Тогда положим х₀ = 0 и из (14.1) найдем у₀ = –С/В. Применяя теперь лемму 14.4, получаем:

Ах + Ву + С = 0 Û

(14.5) А(х–х₀) + В(у–у₀) = 0 Û

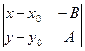= 0.

Но последнее равенство – это каноническое уравнение прямой l = [M₀(x₀,y₀), l(–B,A)] Эту же прямую, следовательно, задает и равносильное ему уравнение (14.1). ð

(14.6) Замечание. Из проведенного доказательства следует, что вектор l(–B,A) будет для прямой (14.1) направляющим (условие (14.2) гарантирует, что он – ненулевой). Это полезно иметь в виду при решении задач.

2. Уравнение центрального пучка. Центральным пучком прямых называется совокупность всех прямых данной плоскости, проходящих через данную ее точку (называемую центром пучка). Доказывая теорему 14.3, мы заодно показали, что если прямая, заданная уравнением (14.1), входит в пучок с центром М₀(х₀,у₀), то она же задается и уравнением (14.5), и обратно, всякое уравнение вида (14.5) при А² + В² ¹ 0 задает некоторую прямую этого пучка. Стало быть, уравнение (14.5) можно (если считать А и В параметрами) понимать как уравнение пучка прямых с центром М₀.

3. Взаимное расположение двух прямых на плоскости. Пусть в некоторой АСК на плоскости заданы общими уравнениями две прямые:

и

l₁: A₁x + B₁y + C₁ = 0 (*)

l₂: A₂x + B₂y + C₂ = 0 (**).

Поставим задачу: не рисуя прямых l₁ и l₂, установить их взаимное расположение по уравнениям (*) и (**). Для начала заметим, что векторы l₁(–B₁,A₁) и l₂(–B₂,A₂) будут для данных прямых направляющими. Поэтому любой признак коллинеарности этих векторов будет в то же время и признаком параллельности (в широком смысле) данных прямых. В частности, прямые (*) и (**) параллельны в широком смысле тогда и только тогда, когда

(14.7) существует такое число k ¹ 0, что А₂ = kA₁, В₂ = kВ₁

или

или

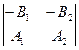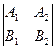(14.7') = 0 Û = 0,

(14.7'') 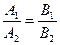(А₂ ¹ 0, В₂ = 0).

Иначе говоря, прямые (*) и (**) параллельны в широком смысле тогда и только тогда, когда коэффициенты при х и у в их общих уравнениях пропорциональны.

Пучком параллельных прямых называется совокупность всех прямых данной плоскости, параллельных данной ее прямой. Доказанный признак параллельности позволяет вывести уравнение такого пучка. Именно, справедлива

(14.8) Теорема. Все прямые плоскости, параллельные прямой (*), и только они, задаются уравнением

(14.9) A₁x + B₁y + C = 0,

при всевозможных действительных значениях параметра С.

ð То, что всякое уравнение вида 14.9 задает прямую, параллельную l₁, вытекает прямо из признака параллельности 14.7. Обратно, если прямая (**) параллельна l₁, ее уравнение в силу (14.7) можно записать в виде kA₁х +kВ₁у + С₂ = 0. Поделив обе части последнего уравнения на k, и положив С = С₂/k, получим уравнение (14.9). ð

Теперь установим признак совпадения двух прямых.

(14.10) Теорема. Прямые (*) и (**) совпадают тогда и только тогда, когда все коэффициенты в их общих уравнениях пропорциональны, т.е. существует такое действительное число k ¹ 0, что

(14.11) А₂ = kA₁, В₂ = kВ₁, С₂ = kС₁.

ð Если выполнены равенства (14.11), то уравнения (*) и (**) равносильны (ибо первое получается из второго делением обеих частей на k), и, стало быть, задают одну и ту же прямую. Обратно, пусть прямые (*) и (**) совпадают. Тогда они параллельны в широком смысле, и, по доказанному выше, существует такое число k ¹ 0, что А₂ = kA₁ и В₂ = kВ₁. Возьмем точку М₀(х₀,у₀), лежащую на прямой l₁. По условию она же лежит и на прямой l₂. Подставив ее координаты в уравнения (*) и (**) и выразив из них свободные члены, получим: С₂ = –(А₂х₀+В₂y₀) = –k(А₁х₀+В₁y₀) = kC₁. ð

Если А₂, В₂, С₂ ¹ 0, то условие (14.11) можно переписать в "опасной" форме:

(14.12) .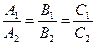

Доказанные признаки позволяют установить геометрический смысл коэффициентов общего уравнения прямой.

(14.13) Теорема. Прямая l, заданная уравнением Ах + Ву + С = 0, параллельна Ох тогда и только тогда, когда А = 0, параллельна Оу тогда и только тогда, когда В = 0 и проходит через начало координат тогда и только тогда, когда С = 0.

ð Ось абсцисс задается уравнением 0х + 1у + 0 = 0. Поэтому l || Ox Û 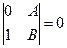Û А = 0. Второе утверждение теоремы доказывается аналогично, а третье проверяется простой подстановкой. ð

4. Геометрический смысл неравенств первой степени с двумя переменными.

(14.14) Теорема. Каждое из двух неравенств:

и

(14.15+) Ах + Ву + С > 0

(14.15–) Ах + Ву + С < 0

задает в АСК на плоскости одну из полуплоскостей, на которые разбивает плоскость прямая l, заданная уравнением Ах + Ву + С = 0.

ð Назовем точки, удовлетворяющие неравенствам (14.15+) и (14.15–), соответственно "положительными" и "отрицательными". Как известно, точки лежат по разные стороны от прямой тогда и только тогда, когда соединяющий их отрезок пересекает прямую. Поэтому нам достаточно доказать, что отрезок, концы которого не лежат на прямой, пересекает ее тогда и только тогда, когда его концы имеют разные знаки. Для этого возьмем точки М₁(х₁,у₁) и М₂(х₂,у₂), не лежащие на l, и посмотрим в каком отношении l делит отрезок [М₁М₂] точка М(х,у) пересечения прямых (М₁М₂) и l. Поскольку точка М лежит на прямой l, а ее координаты находятся по формулам (10.10), имеем:

А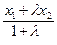 + В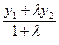 + С = 0 Û (Ах₁ + Ву₁ + С) + l(Ах₂ + Ву₂ + С) = 0 Û

.

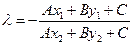Точка М лежит на отрезке [М₁М₂] тогда и только тогда, когда l > 0, а это равносильно тому, что точки М₁ и М₂ имеют разные знаки, что и требовалось доказать. ð

5. Примеры решения задач. (14.16) Задача. Среди точек М₁(1,2), M₂(3,2), M₃(0,4), M₄(5,0) выбрать те, которые лежат от прямой l: х – 2у + 2 = 0 по ту же сторону, что и начало координат.

ð Начало координат – "положительная" точка, ибо 0 + 2´0 + 2 > 0. Поэтому задача сводится к отбору из данных точек "положительных". Проверка показывает, что таковыми являются M₂ и M₄. ð

(14.17) Пересекает ли отрезок с концами М₁(1,2) и M₂(3,2) прямую l из задачи (14.16)?

ð Да, ибо его концы имеют разные знаки. ð

(14.18) Задача. Написать уравнение прямой, проходящей через точку М₁(1,2) параллельно прямой l из задачи (14.16).

ð Искомая прямая входит в пучок прямых, параллельных прямой l. По теореме 14.8 ее можно задать уравнением вида х – 2у + С = 0. Подставляя в него координаты точки М₁, находим, что С = 3. ð

(14.19) Задача. Найти координаты точки пересечения двух прямых, заданных в АСК общими уравнениями.

ð Достаточно составить и решить систему из уравнений этих прямых. ð

(14.20) Задача. Найти координаты (х,у) точки пересечения прямых l из задачи (14.16) и m: x = 1 + 4t, y = 2 – t (*).

ð Достаточно выяснить, при каком значении параметра t точка, движущаяся по закону (*), окажется на прямой l, т.е., решить уравнение 1 + 4t –2(2 – t) + 2 = 0. Решая, получаем t = 1/6, откуда х = 10/6, у = 11/6. ð

(14.21) Задача. Написать уравнение прямой, проходящей через данную точку М(х₀,у₀) и точку N пересечения двух данных прямых.

ð Первый способ. Найдем координаты точки пересечения прямых, а потом напишем уравнение прямой, проходящей через две данные точки.

Второй способ. Заметим, что искомая прямая входит в пучок с центром в точке М. Найдем координаты (х₁, у₁) точки N. Прямая пучка, заданного уравнением (14.5), проходит через точку N при таких А и В, что А(х₁–х₀) + В(у₁–у₀) = 0. При х₁–х₀ ¹ 0 подойдут, например, А = 1, В = (у₀–у₁)/(х₁–х₀), а при х₁–х₀ = 0 годятся А = 1, В = 0. ð

6. Алгебраические линии. Прямая, как линия первого порядка. Одночленом от двух переменных х и у называется выражение вида ах^myⁿ, где а – действительное число, не равное 0, а m и n – натуральные числа. Сумма m+n называется степенью одночлена ах^myⁿ. Многочленом от двух переменных х и у называется сумма конечного числа одночленов от этих переменных, а степенью многочлена – наибольшая из степеней составляющих его одночленов.

Алгебраической линией называется фигура, которую в некоторой АСК на плоскости можно задать уравнением вида F(x,y) = 0, где F – некоторый многочлен от х и у. Иначе говоря, алгебраическая линия – это фигура, являющаяся множеством всех корней некоторого многочлена от двух переменных. Наименьшая возможная степень такого многочлена называется порядком данной кривой. [18] Из теоремы 4.3 немедленно следует

(14.22) Теорема. Алгебраические линии первого порядка – это прямые, и только они.

(14.23) Следствие. Окружность есть алгебраическая кривая второго порядка.

ð Окружность – не прямая, поэтому в силу (14.22) ее порядок выше первого. С другой стороны, он не выше второго, ибо окружность задается уравнением второй степени. ð

Алгебраические линии второго порядка мы подробно изучим в главе 4.