ТЕМА 5. АНАЛИЗ РЯДОВ РАСПРЕДЕЛЕНИЯ
Среди простых группировок особо выделяют ряды распределения.
Рядом распределения в статистике называется упорядоченное распределение единиц сово-
купности на группы по какому-либо признаку. В зависимости от признака положенного в основание ряда распределения различают атрибутивные и вариационные ряды распределения.
Ряды распределения, построенные по описательному признаку, называются атрибутивными рядами. В этом случае ряд распределения составляют отдельные группы, указываемые их наименованием, и численность или удельный вес каждой группы, указываемый в процентах к итогу.
Ряды распределения, построенные по количественному признаку, называются вариационными рядами.
В вариационном ряду различают два элемента: варианты и частоты.
Вариантами (х) называются отдельные значения группировочного признака, которые он принимает в вариационном ряду, т.е. конкретные числовые значения вариационного признака.
Числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения, называются частотами (f). Частоты могут быть даны и как относительные величины структуры (в процентах, или долях единицы, или в промилле). В этом случае их называют частостями.
Сумма всех частот определяет численность всей совокупности, т.е. ее объем (N).
По своей конструкции вариационный ряд состоит из двух столбцов: один столбец - значения варьирующего признака, другой - частоты или частости. Пример вариационного ряда приведен в табл. 5.1.
Таблица 5.1
Пример дискретного вариационного ряда
| Варианта xi | Частота fi |
| x1 x2 … xn | f1 f2 … fn |
| Всего | 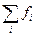 (или N) (или N) |
Вариационные ряды по способу построения бывают двух видов: дискретные и интервальные.
Дискретные вариационные ряды характеризуются тем, что варианты в них имеют значения целых чисел. Например, распределение квартир жилого дома по числу проживающих в них, представленное в табл. 5.2.
Таблица 5.2
Распределение квартир жилого дома по числу проживающих в них
| Число живущих в квартире (х), чел. | Всего | |||||||
| Число квартир (f) |
Если число вариант велико или признак имеет непрерывную вариацию, то объединение отдельных наблюдений в группы возможно лишь на базе интервала.
Интервальные вариационные ряды характеризуются тем, что значения вариант в них заданы в виде интервалов (см. табл. 5.3).
Приведенный в табл. 5.3. вариационный ряд показывает, что наиболее многочисленную группу составляют рабочие, получающие заработную плату от 620 до 670 грн. в месяц. В группах выше и ниже этой группы численность рабочих убывает, причем в группах с более высокой заработной платой число рабочих больше. Так, число рабочих в группах, получающих заработную плату 670 грн. и выше, составляет 41 % (22+16+3), а в группах ниже 620 грн. – 30 % (2+6+10+12).
Если вариационный ряд имеет группы с неравными интервалами, то частоты в отдельных интервалах непосредственно не сопоставимы, так как зависят от ширины интервала. Для того, чтобы частоты можно было бы сравнить исчисляют плотность распределения – частоту (т.е. число единиц совокупности), рассчитанную на единицу ширины интервала.
Таблица 5.3.
Распределение рабочих по размеру месячной заработной платы
| Размеры заработной платы (х), грн. | Численность рабочих (f) | |
| чел. (в абсолютных цифрах) | % (в процентах к итогу) | |
| 420-470 | ||
| 470-520 | ||
| 520-570 | ||
| 570-620 | ||
| 620-670 | ||
| 670-720 | ||
| 720-770 | ||
| 770-820 | ||
| Итого |
Для изображения вариационных рядов применяются линейные и плоскостные диаграммы, построенные в прямоугольной системе координат.
При дискретной вариации признака графиком вариационного ряда служит полигон распределения. Полигон распределения представляет собой замкнутый многоугольник (или ломаную линию), абсциссами вершин которого являются значения варьирующего признака, а ординатами – соответствующие им частоты.
Графическим изображением интервальных вариационных рядов служит гистограмма. Для построения гистограммы по оси абсцисс в соответствии с принятым масштабом откладывают границы равных интервалов. Эти интервалы являются основаниями прямоугольников, площади которых равны (при h =1) либо пропорциональны частотам или частностям распределения в соответствующих интервалах. Гистограмма может быть преобразована в полигон распределения если найти середины сторон прямоугольников и затем эти точки соединить.
При неравных интервалах гистограмма строится только по плотности распределения.
Примеры полигона распределения и гистограммы, построенные по данным табл. 5.2 и 5.3, приведены на рис. 5.1.
 f f
f f



 25 - 150 -
25 - 150 -
 |


 20 - 120 -
20 - 120 -
15 - 90 -
 |


 10 - 60 -
10 - 60 -
 |  | ||


 5 - 30 -
5 - 30 -
 | |||||||
 |  |  | |||||


 ׀ ׀ ׀ ׀ ׀ ׀ ׀ Х // Х
׀ ׀ ׀ ׀ ׀ ׀ ׀ Х // Х
0 1 2 3 4 5 6 7 0 420 520 620 720 820
а) б)
Рис. 5.1. Полигон распределения квартир жилого дома по числу проживающих в них (а) и гистограмма (полигон распределения), отражающая распределение рабочих по размеру месячной заработной платы (б)
Для иллюстрации рядов распределения используются также кумуляты и огивы. Для их построения на оси абсцисс отмечаются значения дискретного признака (или концы интервалов), а на оси ординат – нарастающие итоги частот (кумулята) или частостей (огива), соответствующих этим значениям признака. Ордината кумулятивного графика показывает, сколько единиц или какая часть совокупности имеет значения признака, не превосходящее указанного на оси абсцисс.
Кумулята распределения квартир по числу живущих в них приведена на рис. 5.2.
 f
f

 50-
50-

 40-
40-
30-
20-

10-



 ׀ ׀ ׀ ׀ ׀ ׀ ׀
׀ ׀ ׀ ׀ ׀ ׀ ׀
0 1 2 3 4 5 6 7 Х
Рис. 5.2. Кумулята распределения квартир по числу живущих
Вариационные ряды дают возможность установить характер распределения единиц совокупности по тому или иному количественному признаку с помощью расчета четырех видов характеристик (показателей), приведенных на рис. 5.3.

Рис. 5.3. Основные характеристики ряда распределения
 2014-01-25
2014-01-25 1708
1708
