Системы взаимосвязанных индексов
Индексный метод широко используется для анализа роли отдельных факторов в динамике сложного экономического явления, изменение которого обусловлено действием нескольких факторов, выступающих сомножителями. Выявление и количественная оценка влияния отдельных факторов на изменение сложного явления – одна из важных задач, стоящих перед индексным методом.
Рассмотренная в п. 12.2 динамика товарооборота зависит от динамики физической массы реализуемых товаров и уровня цен на них. Связь между изменением объема товарооборота, выступающего в качестве результативного показателя, количеством проданных товаров и уровнем их цен, являющихся факторными показателями, находит отражение в системе взаимосвязанных индексов товарооборота:
Iqp = Iq ∙ Ip.
Подобные модели – не что иное, как факторные модели типа Х = ab, где Х – результативный признак, a и b – показатели-факторы. В таких системах считается, что все другие причины изменения результативного признака в той или иной мере учтены в выделенных факторах, а построенная модель адекватна экономическому содержанию изучаемого явления. Количество факторов, включаемых в систему, определяют ее как двухфакторную, трехфакторную или многофакторную модель.
Отметим, как связаны между собой результативный показатель и факторы, так же связаны между собой и соответствующие индексы: IХ = Ia ∙ Ib.
Индексы Ia и Ib являются субиндексами индекса IХ.
Для того чтобы сформировать систему общих индексов, т.е., чтобы произведение двух взаимосвязанных индексов давало итоговый показатель динамики, следует соизмерители (веса) в индексах брать на уровнях разных периодов (см. п. 12.2).
Безусловным преимуществом индексных систем является возможность их использования для определения не только относительных показателей влияния отдельных факторов на результативный признак, а и возможность определить на их основе абсолютные величины изменения этого показателя в результате действия указанных факторов.
Абсолютный прирост результативного признака раскладывается на столько же частей, на сколько факторов-сомножителей раскладывается этот показатель.
Абсолютный прирост за счет конкретного фактора рассчитывается как разница между числителем и знаменателем субиндекса этого фактора.
Индексную систему часто используют для определения третьего показателя, если известны два других, входящих в систему.
При изучении динамики показателей деятельности предприятий и других явлений возникает необходимость определить индексы за более чем два периода. В таких случаях индексы могут рассчитываться как на основе постоянной, так и переменной баз сравнения.
Если сравнивают размер явления в различные периоды с состоянием того же явления в какой-то определенный период, то получают систему индексов с постоянной базой сравнения – базисные индексы.
Если оценивают относительные изменения уровня изучаемого явления по сравнению с пред-
шествующим периодом, то получают систему индексов с переменной базой сравнения – цепные индексы.
Особенности расчета индивидуальных и общих индексов количественных и качественных показателей на примере расчета базисных и цепных индексов физического объема, цен и товарооборота показаны в табл. 12.2.
Таблица 12.2
Формулы для расчета базисных и цепных индексов
| Индексы | Базисные | Цепные | |
| Физического объема | Индивидуальные | 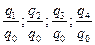
| 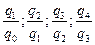
|
| Агрегатные | 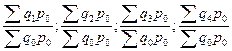
| 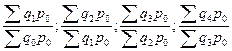
| |
| Цен | Индивидуальные | 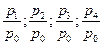
| 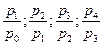
|
| Агрегатные | 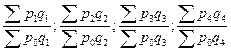
| 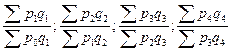
| |
| Товарооборота | Индивидуальные | 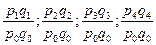
| 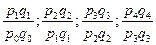
|
| Агрегатные | 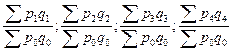
| 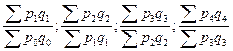
|
Для индивидуальных индексов цен, физического объема и индексов стоимости продукции справедливо (состоящее из двух частей):
1) произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода, т.е. i4/0 = i1/0 ∙ i2/1 ∙ i3/2 ∙ i4/3;
2) отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода, например, i4/3 = i4/0 / i3/0.
Это правило позволяет применять так называемый цепной метод, т.е. находить неизвестный ряд базисных индексов по известным цепным и наоборот.
Применение цепного метода исчисления индексов для общих индексов возможно только для агрегатных индексов физического объема с постоянными соизмерителями.
Если при исчислении цепных индексов физического объема, соизмеритель (цена) принимается на уровне одного и того же периода (см. табл. 12.2), то для агрегатных индексов физического объема действуют те же правила, что и для индивидуальных индексов.
Например, имея два базисных агрегатных индекса физического объема с постоянными соизмерителями, можно получить цепной индекс отчетного периода, разделив базисный индекс отчетного периода на базисный индекс предыдущего периода: I4/0 / I3/0 = I4/3.
Базисный индекс физического объема отчетного периода может быть получен перемножением соответствующих цепных индексов, если соизмеритель (цена) принимается на уровне одного и того же периода: I4/0 = I1/0 ∙ I2/1 ∙ I3/2 ∙ I4/3.
Использование цепного метода для агрегатных индексов физического объема оказалось возможным благодаря применению в качестве соизмерителя фиксированных (соизмеримых, сопоставимых) цен.
Агрегатные индексы качественных показателей всегда является индексами с переменными весами, т.к. количество продукции каждый раз принимается на уровне отчетного периода. Поэтому цепной метод расчета индексов не применим к агрегатным индексам качественных показателей.
 2014-01-25
2014-01-25 1008
1008







