Рядами динамики называют показатели, уровни (у) которых представляют изменение явления (численности, объемов) во времени.
Необходимо четко представлять себе виды рядов динамики, расчет среднего уровня в зависимости от вида ряда динамики, а также систему показателей анализа динамических рядов (2, с. 115-206; 3, с. 101-118) Средний уровень ряда исчисляется:
- в интервальном, периодическом ряду динамики по формуле средней арифметической:
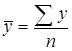 ,
,
где 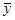 - средний уровень;
- средний уровень;
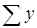 - сумма уровней ряда;
- сумма уровней ряда;
п - число уровней ряда.
- в моментном динамическом ряду с равными интервалами времени между датами средний уровень ряда вычисляется по формуле средней хронологической (2, с. 165)
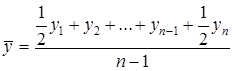
где y1, y2, … yn – уровни моментного ряда динамики (1-й, 2-й,... n-й);
n - число уровней.
Следует знать, что система показателей рядов динамики может быть исчислена базисным (сравнения последующего уровня – уi с начальным уровнем – y1) и цепным (сравнения каждого последующего уровня с предыдущим – yi-1) (2, с. 161-165; 3, с.104-109) методами.
Формулы расчета показателей анализа рядов динамики изложен в таблице.
Таблица 1.
| Показатели анализа рядов динамики | Формулы расчета | |
| базисным методом | ценным методом | |
| 1. Абсолютное изменение | Δб=yi – y1 | Δц = yi – yi-1 |
| 2. Темпы роста | 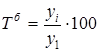
| 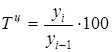
|
| 3. Коэффициенты роста | 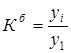
| 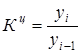
|
| 4. Темпы прироста | tб = Тб - 100,0 | tц = Тц - 100,0 |
Особое внимание следует обратить студентам на расчет таких показателей анализа рядов динамики:
1) абсолютное значение 1% прироста (снижения)
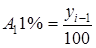 или
или 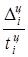 ;
;
2) средний абсолютный прирост (снижение)
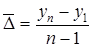
где 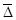 - средний абсолютный прирост (уменьшение);
- средний абсолютный прирост (уменьшение);
yi-1 - любой последующий уровень ряда, включая и первый;
уn - последний уровень ряда.
3) средний годовой коэффициент (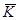 ) или темп (
) или темп (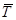 ) изменения за период, применяя среднюю геометрическую формулу;
) изменения за период, применяя среднюю геометрическую формулу;
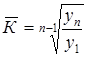 , откуда
, откуда 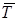 =
=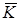 · 100,
· 100,
а потом исчисляют среднегодовой темп прироста (снижения) по формуле:
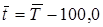
 2014-01-25
2014-01-25 728
728








